
【题目】如图1,在平面直角坐标系中,直线y=x﹣1与抛物线y=﹣x2+bx+c交于A、B两点,其中A(m,0)、B(4,n),该抛物线与y轴交于点C,与x轴交于另一点D.
(1)求m、n的值及该抛物线的解析式;
(2)如图2,若点P为线段AD上的一动点(不与A、D重合),分别以AP、DP为斜边,在直线AD的同侧作等腰直角△APM和等腰直角△DPN,连接MN,试确定△MPN面积最大时P点的坐标;
(3)如图3,连接BD、CD,在线段CD上是否存在点Q,使得以A、D、Q为顶点的三角形与△ABD相似,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
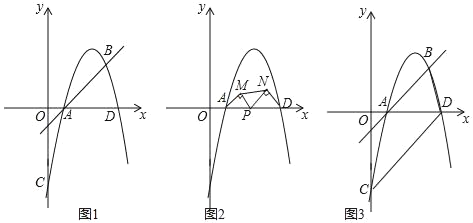
【答案】(1)m=1,n=3, y=﹣x2+6x﹣5;(2) 当m=2,即AP=2时,S△MPN最大,此时OP=3,即P(3,0);(3)存在,点Q的坐标为(2,﹣3)或(![]() ),理由见解析
),理由见解析
【解析】
(1)把A与B坐标代入一次函数解析式求出m与n的值,确定出A与B坐标,代入二次函数解析式求出b与c的值即可;
(2)由等腰直角△APM和等腰直角△DPN,得到∠MPN为直角,由两直角边乘积的一半表示出三角形MPN面积,利用二次函数性质确定出三角形面积最大时P的坐标即可;
(3)存在,分两种情况,根据相似得比例,求出AQ的长,利用两点间的距离公式求出Q坐标即可.
解:(1)把A(m,0),B(4,n)代入y=x﹣1得:m=1,n=3,
∴A(1,0),B(4,3),
∵y=﹣x2+bx+c经过点A与点B,
∴![]() ,
,
解得:![]() ,
,
则二次函数解析式为y=﹣x2+6x﹣5;
(2)如图2,△APM与△DPN都为等腰直角三角形,
∴∠APM=∠DPN=45°,
∴∠MPN=90°,
∴△MPN为直角三角形,
令﹣x2+6x﹣5=0,得到x=1或x=5,
∴D(5,0),即DA=5﹣1=4,
设AP=m,则有DP=4﹣m,
∴PM=![]() m,PN=
m,PN=![]() (4﹣m),
(4﹣m),
∴S△MPN=![]() PMPN=
PMPN=![]() ×
×![]() m×
m×![]() (4﹣m)=﹣
(4﹣m)=﹣![]() m2+m=﹣
m2+m=﹣![]() (m﹣2)2+1,
(m﹣2)2+1,
∴当m=2,即AP=2时,S△MPN最大,此时OP=3,即P(3,0);
(3)存在,
易得直线CD解析式为y=x﹣5,设Q(x,x﹣5),
由题意得:∠BAD=∠ADC=45°,
当△ABD∽△/span>DAQ时,![]() ,即
,即![]() ,
,
解得:AQ=![]() ,
,
由两点间的距离公式得:(x﹣1)2+(x﹣5)2=![]() ,
,
解得:x=![]() 或x=
或x=![]() ,此时Q(
,此时Q(![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() )(舍去);
)(舍去);
当△ABD∽△DQA时,![]() =1,即AQ=
=1,即AQ=![]() ,
,
∴(x﹣1)2+(x﹣5)2=10,
解得:x=2或x=4,此时Q(2,﹣3)或(4,﹣1)(舍去),
综上,点Q的坐标为(2,﹣3)或(![]() ).
).


科目:初中数学 来源: 题型:
【题目】某市为解决部分市民冬季集中取暖问题,需铺设一条长4000米的管道,为尽量减少施工对交通造成的影响,施工时“…”,设实际每天铺设管道x米,则可得方程![]() =20,根据此情景,题中用“…”表示的缺失的条件应补为( )
=20,根据此情景,题中用“…”表示的缺失的条件应补为( )
A. 每天比原计划多铺设10米,结果延期20天完成
B. 每天比原计划少铺设10米,结果延期20天完成
C. 每天比原计划多铺设10米,结果提前20天完成
D. 每天比原计划少铺设10米,结果提前20天完成
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD交于点O,E为AB的中点,G为BC延长线上一点,射线EO与∠ACG的角平分线交于点F,若AB=8,BC=6,则线段EF的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,∠A=120°,点E是BC边的中点,点P是对角线BD上一动点,设PD的长度为x,PE与PC的长度和为y,图2是y关于x的函数图象,其中H是图象上的最低点,则a+b的值为( )
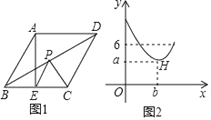
A.7![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
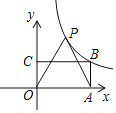
【题目】如图,矩形OABC的顶点A,C分别在x轴,y轴上,顶点B在第一象限,AB=1.将线段OA绕点O按逆时针方向旋转60°得到线段OP,连接AP,反比例函数![]() (k≠0)的图象经过P,B两点,则k的值为______________.
(k≠0)的图象经过P,B两点,则k的值为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
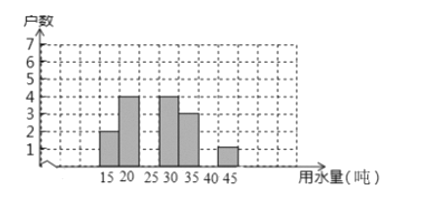
【题目】下表是2019年三月份某居民小区随机抽取20户居民的用水情况:
用水量/吨 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
户数 | 2 | 4 | m | 4 | 3 | 0 | 1 |
(1)求出m= ,补充画出这20户家庭三月份用电量的条形统计图;
(2)据上表中有关信息,计算或找出下表中的统计量,并将结果填入表中:
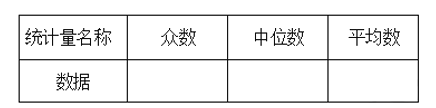
(3)为了倡导“节约用水,绿色环保”的意识,台州市自来水公司实行“梯级用水、分类计费”,价格表如下:

如果该小区有500户家庭,根据以上数据,请估算该小区三月份有多少户家庭在ⅠI级标准?并估算这些级用水户的总水费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
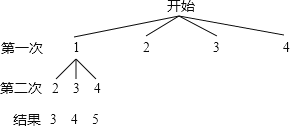
【题目】在不透明的袋子中有四张标着数字1,2,3,4的卡片,这些卡片除数字外都相同.小芸同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.如图是她所画的树状图的一部分.
(1)由如图分析,小芸的游戏规则是:从袋子中随机抽出一张卡片后 (填“放回”或“不放回”),再随机抽出一张卡片;
(2)帮小芸完成树状图;
(3)求小芸两次抽到的数字之和为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
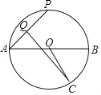
【题目】如图,AB为⊙O的直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为( )
A. 3 B. 1+![]() C. 1+3
C. 1+3![]() D. 1+
D. 1+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载,某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于24米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
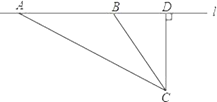
(1)求AB的长(结果保留根号);
(2)已知本路段对校车限速为45千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com