
分析 根据根与系数的关系,得出x1+x2和x1•x2,再化简(2x1+x2)(x1+2x2)=6,求得m即可.
解答 解:∵x1、x2是关于x的方程x2-2mx+m2-1=0的两根,
∴x1+x2=2m,x1•x2=m2-1,
∵(2x1+x2)(x1+2x2)=6,
∴2x12+4x1x2+x1x2+2x22=6,
即2x12+5x1x2+2x22=6,
∴2(x1+x2)2+x1x2=6,
∴8m2+m2-7=0,
解得m=±$\frac{\sqrt{7}}{3}$,
当m=±$\frac{\sqrt{7}}{3}$时,方程有实数根,
∴m的值为±$\frac{\sqrt{7}}{3}$.
点评 本题主要考查了根与系数的关系的知识,解答本题的关键是掌握一元二次方程两根之和与两根之积与系数的关系,此题难度不大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是( )
在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是( )| A. | 64m2 | B. | 32m2 | C. | 128m2 | D. | 96m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
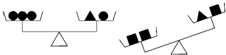
| A. | ●、▲、■ | B. | ■、▲、● | C. | ▲、■、● | D. | ■、●、▲ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com