
【题目】如图,P是等边△ABC内部一点,∠APB,∠BPC,∠CPA的大小之比是5:6:7,则以PA、PB、PC为边的三角形的三个内角的大小之比是(从小到大)( )
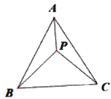
A.2:3:4B.4:5:6C.3:4:5D.不确定
【答案】A
【解析】
将△APB绕A点逆时针旋转60°得△AP′C,可得△AP′P是等边三角形,PP′=AP,所以△P′CP的三边长分别为PA,PB,PC;再求出∠APB=100°,∠BPC=120°,∠CPA=140°,这样可分别求出∠PP′C=40°,∠P′PC=80°,∠PCP′=60°,即可得到答案.
如图,将△APB绕A点逆时针旋转60°得△AP′C,显然有△AP′C≌△APB,连PP′,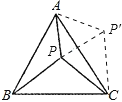
∵AP′=AP,∠P′AP=60°,
∴△AP′P是等边三角形,
∴PP′=AP,
∵P′C=PB,
∴△P′CP的三边长分别为PA,PB,PC,
∵∠APB+∠BPC+∠CPA=360°,∠APB:∠BPC:∠CPA=5:6:7,
∴∠APB=100°,∠BPC=120°,∠CPA=140°,
∴∠PP′C=∠AP′C∠AP′P=∠APB∠AP′P=100°-60°=40°,
∠P′PC=∠APC-∠APP′=140°-60°=80°
∠PCP′=180°-(40°+80°)=60°,
∴∠PP′C:∠PCP′:∠P′PC=2:3:4.
故选A.


科目:初中数学 来源: 题型:
【题目】某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 、
、![]() ,点
,点![]() 坐标为
坐标为![]() .
.
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 抛物线的顶点为
抛物线的顶点为![]() ,在
,在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 最小,并求出点
最小,并求出点![]() 的坐标;
的坐标;
![]() 点
点![]() 是线段
是线段![]() 上的动点,过点
上的动点,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .当
.当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
![]() 若平行于
若平行于![]() 轴的动直线
轴的动直线![]() 与该抛物线交于点
与该抛物线交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() .问:是否存在这样的直线
.问:是否存在这样的直线![]() ,使得
,使得![]() 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知将边长分别为a和2b(a>b)的长方形分割成四个全等的直角三角形,如图1,再用这四个三角形拼成如图2所示的正方形,中间形成一个正方形的空洞.经测量得长方形的面积为24,正方形的边长为5.试通过你获取的信息,求a2+b2和a2﹣b2的值.
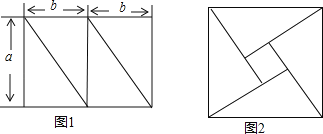
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列问题:
(1)若 n(n≠0)是关于 ![]() 的方程 x+mx-2n=0的根,求 m+n的值;
的方程 x+mx-2n=0的根,求 m+n的值;
(2)已知 ![]() ,
, ![]() 为实数,且 y=2
为实数,且 y=2![]() ,求 2x-3y的值.
,求 2x-3y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=![]() (k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,
(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,![]() ),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是( )
),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是( )

A. (![]() ,0)B. (
,0)B. (![]() ,0)C. (
,0)C. (![]() ,0)D. (
,0)D. (![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知函数y=![]() (k>0,x>0)的图象与一次函数y=mx+5(m<0)的图象相交不同的点A、B,过点A作AD⊥x轴于点D,连接AO,其中点A的横坐标为x0,△AOD的面积为2.
(k>0,x>0)的图象与一次函数y=mx+5(m<0)的图象相交不同的点A、B,过点A作AD⊥x轴于点D,连接AO,其中点A的横坐标为x0,△AOD的面积为2.
(1)求k的值及x0=4时m的值;
(2)记[x]表示为不超过x的最大整数,例如:[1.4]=1,[2]=2,设t=ODDC,若﹣![]() <m<﹣
<m<﹣![]() ,求[m2t]值.
,求[m2t]值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com