
【题目】完成下列问题:
(1)若 n(n≠0)是关于 ![]() 的方程 x+mx-2n=0的根,求 m+n的值;
的方程 x+mx-2n=0的根,求 m+n的值;
(2)已知 ![]() ,
, ![]() 为实数,且 y=2
为实数,且 y=2![]() ,求 2x-3y的值.
,求 2x-3y的值.
科目:初中数学 来源: 题型:
【题目】如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在ΔABC外的点![]() 处,若∠1=20°,则∠2的度数为( )
处,若∠1=20°,则∠2的度数为( )

A. 80°B. 90°
C. 100°D. 110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设一个三角形的三边分别是3,13m,8.

(1)求m的取值范围;
(2)是否存在整数m使三角形的周长为偶数?若存在,求出三角形的周长;若不存在,说明理由;
(3)如图,在(2)的条件下,当AB=8,AC=13m,BC=3时,若D是AB的中点,连CD,P是CD上动点(不与C,D重合,当P在线段CD上运动时,有两个式子):①![]() ;②
;②![]() ,其中有一个的值不变,另一个的值改变。问题:
,其中有一个的值不变,另一个的值改变。问题:
A.请判断出谁不变,谁改变;
B.若不变的求出其值,若改变的求出变化的范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边△ABC内部一点,∠APB,∠BPC,∠CPA的大小之比是5:6:7,则以PA、PB、PC为边的三角形的三个内角的大小之比是(从小到大)( )
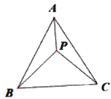
A.2:3:4B.4:5:6C.3:4:5D.不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列文字:我们知道对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)= a2+3ab+2b2.请解答下列问题:
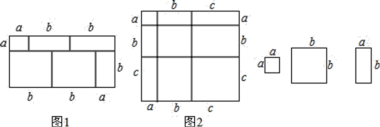
(1)写出图2中所表示的数学等式 ;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=9,ab+bc+ac=29,求a 2+b2+c2的值;
(3)小明同学打算用x张边长为a和y张边长为b的小正方形,z张相邻两边长分别为a、b的长方形纸片拼出了一个面积为(3a+5b)(4a+7b)的长方形,那么他总共需要多少张纸片?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,A(-a,0),B(b,0),C(0,c),且满足![]() .
.
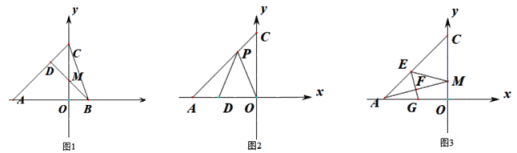
(1)如图1,过B作BD⊥AC,交y轴于M,垂足为D,求M点的坐标.
(2)如图2,若a=3![]() ,AC=6,点P为线段AC上一点,D为x轴负半轴上一点,且PD=PO,∠DPO=45°,求点D的坐标.
,AC=6,点P为线段AC上一点,D为x轴负半轴上一点,且PD=PO,∠DPO=45°,求点D的坐标.
(3)如图3,M在OC上,E在AC上,满足∠CME=∠OMA,EF⊥AM交AO于G,垂足为F,试猜想线段OG,OM,CM三者之间的数量关系,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角尺按如图①方式拼接:含30°角的三角尺的长直角边与含45°角的三角尺的斜边恰好重合(在Rt△ABC中,∠ACB=90°,∠BAC=30°;在Rt△ACD中,∠ADC=90°∠DAC=45°)已知AB=2![]() ,P是AC上的一个动点.
,P是AC上的一个动点.

(1)当PD=BC时,求∠PDA的度数;
(2)如图②,若E是CD的中点,求△DEP周长的最小值;
(3)如图③,当DP平分∠ADC时,在△ABC内存在一点Q,使得∠DQC=∠DPC,且CQ=![]() ,求PQ的长.
,求PQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com