
【题目】阅读下列文字:我们知道对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)= a2+3ab+2b2.请解答下列问题:
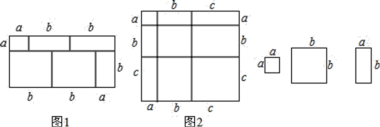
(1)写出图2中所表示的数学等式 ;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=9,ab+bc+ac=29,求a 2+b2+c2的值;
(3)小明同学打算用x张边长为a和y张边长为b的小正方形,z张相邻两边长分别为a、b的长方形纸片拼出了一个面积为(3a+5b)(4a+7b)的长方形,那么他总共需要多少张纸片?
【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;(2)23;(3)88张.
【解析】
(1)直接求得正方形的面积,然后再根据正方形的面积=各矩形的面积之和求解即可;
(2)将a+b+c=9,ab+bc+ac=29代入(1)中得到的关系式,然后进行计算即可;
(3)将(3a+5b)(4a+7b)展开后即可得出答案.
解:(1)正方形的面积可表示为=(a+b+c)2;
正方形的面积=各个矩形的面积之和=a2+b2+c2+2ab+2bc+2ac,
故答案为:(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)∵a+b+c=12,ab+bc+ac=29,
∴由(1)可知:a2+b2+c2=(a+b+c)22(ab+bc+ca)=81-29×2=23,
(3)∵![]() =
=![]() =
=![]()
∴需要边长为a的小正方形12张,变成为b的小正方形35张,邻边为a、b的长方形41张,总共需要12+35+41=88张.


科目:初中数学 来源: 题型:
【题目】徐州至北京的高铁里程约为700km,甲、乙两人从徐州出发,分别乘坐“徐州号”高铁A与“复兴号”高铁B前往北京.已知A车的平均速度比B车的平均速度慢80km/h,A车的行驶时间比B车的行驶时间多40%,两车的行驶时间分别为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
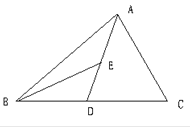
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知将边长分别为a和2b(a>b)的长方形分割成四个全等的直角三角形,如图1,再用这四个三角形拼成如图2所示的正方形,中间形成一个正方形的空洞.经测量得长方形的面积为24,正方形的边长为5.试通过你获取的信息,求a2+b2和a2﹣b2的值.
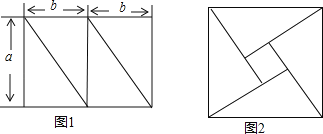
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.

(1)若∠A=60°,求BC的长;
(2)若sinA=![]() ,求AD的长.
,求AD的长.
(注意:本题中的计算过程和结果均保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列问题:
(1)若 n(n≠0)是关于 ![]() 的方程 x+mx-2n=0的根,求 m+n的值;
的方程 x+mx-2n=0的根,求 m+n的值;
(2)已知 ![]() ,
, ![]() 为实数,且 y=2
为实数,且 y=2![]() ,求 2x-3y的值.
,求 2x-3y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的大小;
(2)若CD=3,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,AB=4,点E,F在对角线BD上,AE∥CF.
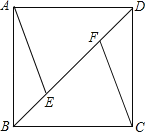
(1)求证:△ABE≌△CDF;
(2)若∠ABE=2∠BAE,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com