
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
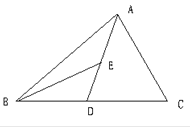
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高为多少?
【答案】(1)55°;(2)作图见解析;(3)4.
【解析】
(1)根据三角形内角与外角的性质解答即可;
(2)过E作BC边的垂线即可;
(3)过A作BC边的垂线AG,再根据三角形中位线定理求解即可.
解:(1)∵∠BED是△ABE的外角,
∴∠BED=∠ABE+∠BAD=15°+40°=55°;
(2)过E作BC边的垂线,F为垂足,则EF为所求;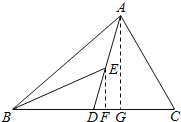
(3)过A作BC边的垂线AG,
∴AD为△ABC的中线,BD=5,
∴BC=2BD=2×5=10,
∵△ABC的面积为40,
∴![]() BCAG=40,即
BCAG=40,即![]() ×10AG=40,解得AG=8,
×10AG=40,解得AG=8,
∵EF⊥BC于F,
∴EF∥AG,
∵E为AD的中点,
∴EF是△AGD的中位线,
∴EF=![]() AG=
AG=![]() ×8=4.
×8=4.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:初中数学 来源: 题型:
【题目】两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了____m,恰好把水喷到F处进行灭火.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).


求(1)抛物线的解析式;
(2)两盏景观灯P1、P2之间的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③a-2b+4c<0;④8a+c>0.其中正确的有____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设一个三角形的三边分别是3,13m,8.

(1)求m的取值范围;
(2)是否存在整数m使三角形的周长为偶数?若存在,求出三角形的周长;若不存在,说明理由;
(3)如图,在(2)的条件下,当AB=8,AC=13m,BC=3时,若D是AB的中点,连CD,P是CD上动点(不与C,D重合,当P在线段CD上运动时,有两个式子):①![]() ;②
;②![]() ,其中有一个的值不变,另一个的值改变。问题:
,其中有一个的值不变,另一个的值改变。问题:
A.请判断出谁不变,谁改变;
B.若不变的求出其值,若改变的求出变化的范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列文字:我们知道对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)= a2+3ab+2b2.请解答下列问题:
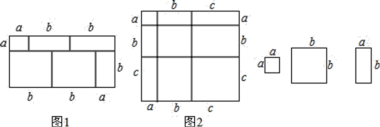
(1)写出图2中所表示的数学等式 ;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=9,ab+bc+ac=29,求a 2+b2+c2的值;
(3)小明同学打算用x张边长为a和y张边长为b的小正方形,z张相邻两边长分别为a、b的长方形纸片拼出了一个面积为(3a+5b)(4a+7b)的长方形,那么他总共需要多少张纸片?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形OABC的边与函数y=![]() (x>0)图象交于E,F两点,且F是BC的中点,则四边形ACFE的面积等于( )
(x>0)图象交于E,F两点,且F是BC的中点,则四边形ACFE的面积等于( )
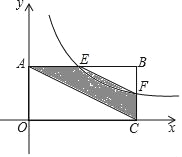
A. 4 B. 6 C. 8 D. 不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com