
【题目】两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了____m,恰好把水喷到F处进行灭火.

【答案】![]()
【解析】设直线AE的解析式为:y=kx+21.2.
把E(20,9.2)代入得,
20k+21.2=9.2,
∴k=-0.6,
∴y=-0.6x+21.2.
把y=6.2代入得,
-0.6x+21.2=6.2,
∴x=25,
∴F(25,6.2).
设抛物线解析式为:y=ax2+bx+1.2,
把E(20,9.2), F(25,6.2)代入得,
![]()
解之得
![]() ,
,
∴y=-0.04x2+1.2x+1.2,
设向上平移0.4m,向左后退了hm, 恰好把水喷到F处进行灭火由题意得
y=-0.04(x+h)2+1.2(x+h)+1.2+0.4,
把F(25,6.2)代入得,
6.2=-0.04×(25+h)2+1.2(25+h)+1.2+0.4,
整理得
h2+20h-10=0,
解之得
![]() ,
, ![]() (舍去).
(舍去).
∴向后退了![]() m
m


科目:初中数学 来源: 题型:
【题目】如图①,已知点D在AB上,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,且M为EC的中点.

(1)连接DM并延长交BC于N,求证:CN=AD;
(2)求证:△BMD为等腰直角三角形;
(3)将△ADE绕点A逆时针旋转90°时(如图②所示位置),其它条件不变,△BMD为等腰直角三角形的结论是否仍成立?若成立,请证明:若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】徐州至北京的高铁里程约为700km,甲、乙两人从徐州出发,分别乘坐“徐州号”高铁A与“复兴号”高铁B前往北京.已知A车的平均速度比B车的平均速度慢80km/h,A车的行驶时间比B车的行驶时间多40%,两车的行驶时间分别为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售某一种新型通讯产品,已知每件产品的进价为4万元,每月销售该种产品的总开支(不含进价)总计11万元.在销售过程中发现,月销售量夕(件)与销售单价x (万元)之间存在着如图所示的一次函数关系、
(1)求y关于x的函数关系式(直接写出结果)
(2)试写出该公司销售该种产品的月获利z(万元)关于销售单价x(万元)的函数关系式、当销售单价x为何值时,月获利最大?并求这个最大值(月获利一月销售额一月销售产品总进价一月总开支)
(3)若公司希望该产品一个月的销售获利不低于5万元,借助(2)中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少万元

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球比赛中,某运动员将在地面上的足球对着球门踢出,图中的抛物线是足球的飞行高度y(m)关于飞行时间x(s)的函数图象(不考虑其它因素),已知足球飞出1s时,足球的飞行高度是2.44m,足球从飞出到落地共用3s.

(1)求y关于x的函数解析式;
(2)足球的飞行高度能否达到4.88 m?请说明理由;
(3)假设没有拦挡,足球将擦着球门左上角射入球门,球门的高为2.44 m(如图所示,足球的大小忽略不计).如果为了能及时将足球扑出,那么足球被踢出时,离球门左边框12m处的守门员至少要在几s内到球门的左边框?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个全等的含30°,60°角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.试判断△EMC的形状,并说明理由.
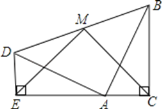
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
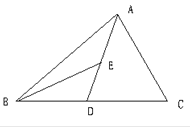
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的大小;
(2)若CD=3,求DF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com