
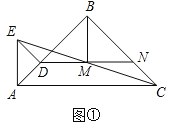
【题目】如图①,已知点D在AB上,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,且M为EC的中点.

(1)连接DM并延长交BC于N,求证:CN=AD;
(2)求证:△BMD为等腰直角三角形;
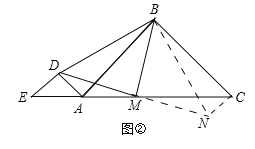
(3)将△ADE绕点A逆时针旋转90°时(如图②所示位置),其它条件不变,△BMD为等腰直角三角形的结论是否仍成立?若成立,请证明:若不成立,请说明理由.
【答案】(1)见解析;(2)见解析;(3)仍成立,见解析;
【解析】
(1)由∠ABC=∠ADE=90°可得DE∥BC,再根据平行线的性质,推出∠DEM=∠MCB,根据ASA推出△EMD≌△CMN,证出CN=ED,因为AD=DE,即可得到CN=AD;
(2)由(1)可知CN=AD,DM=MN,再由AB=AC,可得BD=BN,从而可得△DBN是等腰直角三角形,且BM是底边DN上的中线,再利用等腰三角形的三线合一的性质和直角三角形的性质即可得到△BMD为等腰直角三角形;
(3)作CN∥DE交DM的延长线于N,连接BN,根据平行线的性质求出∠E=∠NCM,根据ASA证△DBA≌△NBC,推出△DBN是等腰直角三角形,根据等腰直角三角形的性质即可推出△BMD为等腰直角三角形.
(1)证明:如图①,
∵∠EDA=∠ABC=90°,
∴DE∥BC,
∴∠DEM=∠MCB,
在△EMD和△CMN中,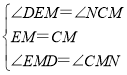 ,
,
∴△EMD≌△CMN(ASA),
∴CN=DE,
∵AD=DE,
∴CN=AD;
(2)证明:由(1)得CN=AD,△EMD≌△CMN,
∴DM=MN,
∵BA=BC,CN=AD,
∴BD=BN,
∴△DBN是等腰直角三角形,且BM是底边的中线,
∴BM⊥DM,BM=![]() DN=DM,
DN=DM,
∴△BMD为等腰直角三角形;
(3)答:△BMD为等腰直角三角形的结论仍成立,
证明:如图②,作CN∥DE交DM的延长线于N,连接BN,
∴∠E=∠MCN=45°,
∵∠DME=∠NMC,EM=CM,
∴△EMD≌△CMN(ASA),
∴CN=DE=DA,MN=MD,
又∵∠DAB=180°-∠DAE-∠BAC=90°,
∠BCN=∠BCM+∠NCM=45°+45°=90°,
∴∠DAB=∠NCB,
在△DBA和△NBC中, ,
,
∴△DBA≌△NBC(SAS),
∴∠DBA=∠NBC,DB=BN,
∴∠DBN=∠ABC=90°,
∴△DBN是等腰直角三角形,且BM是底边的中线,
∴BM⊥DM,∠DBM=![]() ∠DBN=45°=∠BDM,
∠DBN=45°=∠BDM,
∴MB=MD,
∴△BMD为等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】某城市出租汽车收费标准为:![]() 以内(含
以内(含![]() )收费
)收费![]() 元;超出
元;超出![]() 的部分,每千米收费
的部分,每千米收费![]() 元.
元.
(1)写出车费![]() 元与行驶路程x(km)之间的函数关系式(
元与行驶路程x(km)之间的函数关系式(![]() ≥4);
≥4);
(2)某人乘出租汽车行驶了5 km,应付多少车费;
(3)若某人付了![]() 元车费,那么出租车行驶了多远.
元车费,那么出租车行驶了多远.
查看答案和解析>>
科目:初中数学 来源: 题型:
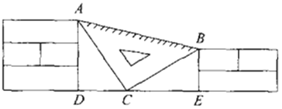
【题目】课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),![]() ,
,![]() ,每块砌墙用的砖块厚度为
,每块砌墙用的砖块厚度为![]() ,小聪很快就知道了两个墙脚之间的距离
,小聪很快就知道了两个墙脚之间的距离![]() 的长为______
的长为______![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】何老师将五顶帽子分别给五位同学戴上,每位同学都知道有三顶白色、两顶黑色,但不知道自己所戴帽子的颜色.现将五位同学分别安排在两个小房子中(如图),不许他们摘下帽子看或回头看,也不许互相交流,经过一段时间,其中一位同学可以最快报出白己所戴帽子的颜色,则该同学的编号是( )
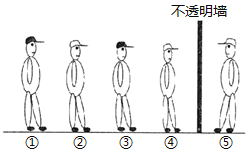
A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=38°,D,E分别为AB,AC上一点,将△BCD,△ADE沿CD,DE翻折,点A,B恰好重合于点P处,则∠ACP=_________.
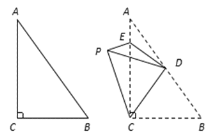
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MBC和∠NCB是△ABC的外角,点O是∠MBC和∠NCB的平分线的交点,点O叫做△ABC的旁心.

(1)已知∠A=100°,那么∠BOC等于多少度;
(2)猜想∠BOC与∠A有什么数量关系?并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题
(1)画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1,并写出点C1的坐标;
(2)画出将△ABC关于原点O对称的图形△A2B2C2,并写出点C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了____m,恰好把水喷到F处进行灭火.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com