
【题目】如图,∠MBC和∠NCB是△ABC的外角,点O是∠MBC和∠NCB的平分线的交点,点O叫做△ABC的旁心.

(1)已知∠A=100°,那么∠BOC等于多少度;
(2)猜想∠BOC与∠A有什么数量关系?并证明你的猜想.
【答案】(1)40;(2)90°-![]() ∠A,见解析.
∠A,见解析.
【解析】
(1)根据BO平分∠MBC,CO平分∠NCB,即可得到∠OBC=![]() ∠MBC,∠OCB=
∠MBC,∠OCB=![]() ∠NCB,利用三角形外角性质,即可得出∠OBC=
∠NCB,利用三角形外角性质,即可得出∠OBC=![]() (∠A+∠ACB),∠OCB=
(∠A+∠ACB),∠OCB=![]() (∠A+∠ABC),再根据∠BOC=180°-∠OBC-∠OCB进行计算即可.
(∠A+∠ABC),再根据∠BOC=180°-∠OBC-∠OCB进行计算即可.
(2)利用(1)中的方法,即可得到∠BOC与∠A的数量关系.
解:(1)∵BO平分∠MBC,CO平分∠NCB,
∴∠OBC=![]() ∠MBC,∠OCB=
∠MBC,∠OCB=![]() ∠NCB,
∠NCB,
∵∠OBC=![]() (∠A+∠ACB),∠OCB=
(∠A+∠ACB),∠OCB=![]() (∠A+∠ABC),
(∠A+∠ABC),
∴∠BOC=180°-∠OBC-∠OCB
=180°-![]() (∠A+∠ACB)-
(∠A+∠ACB)-![]() (∠A+∠ABC)
(∠A+∠ABC)
=180°-![]() (∠A+∠ACB+∠A+∠ABC)
(∠A+∠ACB+∠A+∠ABC)
=180°-![]() (180°+∠A)
(180°+∠A)
=90°-![]() ∠A
∠A
=90°-![]() ×100°
×100°
=40°,
故答案为:40;
(2)猜想:∠BOC=90°-![]() ∠A.
∠A.
证明:∵BO平分∠MBC,CO平分∠NCB,
∴∠OBC=![]() ∠MBC,∠OCB=
∠MBC,∠OCB=![]() ∠NCB,
∠NCB,
∵∠OBC=![]() (∠A+∠ACB),∠OCB=
(∠A+∠ACB),∠OCB=![]() (∠A+∠ABC),
(∠A+∠ABC),
∴∠BOC=180°-∠OBC-∠OCB
=180°-![]() (∠A+∠ACB)-
(∠A+∠ACB)-![]() (∠A+∠ABC)
(∠A+∠ABC)
=180°-![]() (∠A+∠ACB+∠A+∠ABC)
(∠A+∠ACB+∠A+∠ABC)
=180°-![]() (180°+∠A)
(180°+∠A)
=90°-![]() ∠A.
∠A.
故答案为:(1)40;(2)90°-![]() ∠A,见解析.
∠A,见解析.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小强先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(x,y)落在一次函数![]() 图象上的概率;
图象上的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一渔船在海岛![]() 南偏东
南偏东![]() 方向的
方向的![]() 处遇险,测得海岛
处遇险,测得海岛![]() 与
与![]() 的距离为
的距离为![]() 海里,渔船将险情报告给位于
海里,渔船将险情报告给位于![]() 处的救援船后,沿北偏西
处的救援船后,沿北偏西![]() 方向向海岛
方向向海岛![]() 靠近,同时,从
靠近,同时,从![]() 处出发的救援船沿南偏西
处出发的救援船沿南偏西![]() 方向匀速航行,
方向匀速航行,![]() 分钟后,救援船在海岛
分钟后,救援船在海岛![]() 处恰好追上渔船,那么救援船航行的速度为( )
处恰好追上渔船,那么救援船航行的速度为( )

A. 10![]() 海里/小时 B. 30海里/小时 C. 20
海里/小时 B. 30海里/小时 C. 20![]() 海里/小时 D. 30
海里/小时 D. 30![]() 海里/小时
海里/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如果点![]() 的横坐标和纵坐标相等,则称点
的横坐标和纵坐标相等,则称点![]() 为和谐点,例如点
为和谐点,例如点![]() ,
,![]() ,
,![]() ,…都是和谐点,若二次函数
,…都是和谐点,若二次函数![]() 的图象上有且只有一个和谐点
的图象上有且只有一个和谐点![]() ,当
,当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,最大值为
,最大值为![]() ,则
,则![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知点D在AB上,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,且M为EC的中点.

(1)连接DM并延长交BC于N,求证:CN=AD;
(2)求证:△BMD为等腰直角三角形;
(3)将△ADE绕点A逆时针旋转90°时(如图②所示位置),其它条件不变,△BMD为等腰直角三角形的结论是否仍成立?若成立,请证明:若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进的乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,购进这两种玩具的总资金超过960元但不超过1000元,求商场有哪几种具体的进货方案?最多可以购进乙种玩具多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
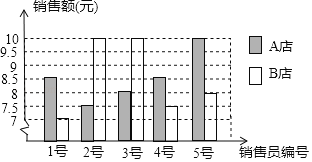
【题目】A、B两店分另选5名销售员某月的销售额(单位:万元)进行分析,数据如下图表(不完整):
平均数 | 中位数 | 众数 | |
A店 | 8.5 |
|
|
B店 |
| 8 | 10 |
(1)根据图a数据填充表格b所缺的数据;
(2)如果A店想让一半以上的销售员达到销售目标,你认为月销售额定为多少合适?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆假期期间,某单位8名领导和320名员工集体外出进行素质拓展活动,准备租用45座大车或30座小车.若租用2辆大车3辆小车共需租车费1700元;若租用3辆大车2辆小车共需租车费1800元
(1)求大、小车每辆的租车费各是多少元?
(2)若每辆车上至少要有一名领导,每个人均有座位,且总租车费用不超过3100元,求最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球比赛中,某运动员将在地面上的足球对着球门踢出,图中的抛物线是足球的飞行高度y(m)关于飞行时间x(s)的函数图象(不考虑其它因素),已知足球飞出1s时,足球的飞行高度是2.44m,足球从飞出到落地共用3s.

(1)求y关于x的函数解析式;
(2)足球的飞行高度能否达到4.88 m?请说明理由;
(3)假设没有拦挡,足球将擦着球门左上角射入球门,球门的高为2.44 m(如图所示,足球的大小忽略不计).如果为了能及时将足球扑出,那么足球被踢出时,离球门左边框12m处的守门员至少要在几s内到球门的左边框?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com