
����Ŀ����������У�ij�˶�Ա���ڵ����ϵ�������������߳���ͼ�е�������������ķ��и߶�y��m�����ڷ���ʱ��x��s���ĺ���ͼ�������������أ�����֪����ɳ�1sʱ������ķ��и߶���2.44m������ӷɳ�����ع���3s��

��1����y����x�ĺ�������ʽ��
��2������ķ��и߶��ܷ�ﵽ4.88 m����˵�����ɣ�
��3������û���������������������Ͻ��������ţ����ŵĸ�Ϊ2.44 m����ͼ��ʾ������Ĵ�С���Բ��ƣ������Ϊ���ܼ�ʱ�������˳�����ô�����߳�ʱ����������߿�12m��������Ա����Ҫ�ڼ�s�ڵ����ŵ���߿�
���𰸡�(1) y=-1.22x2+3.66x ;(2) ���ܣ����ɼ�����;(3)2s.
��������
��1���۲������ߵ�ͼ��ԭ�㣬�����y����x�ĺ�����ϵʽΪy=ax2+bx���ٽ��㣨1��2.44������3,0�����뺯������ʽ���ɽ��
��2����y=4.88���루1���еĺ�������ʽ����һԪ���η��̣����ݷ��̽����������жϡ�
��3����y=2.44���뺯������ʽ�����x��ֵ����������ó�����������x��ֵ�����ɽ��
��1���⣺��y����x�ĺ�����ϵʽΪy=ax2+bx��
�����֪��
��x=1ʱ��y=2.44��
��x=3ʱ��y=0��
�� ![]() ��
��
��![]() ��
��
��y=-1.22x2+3.66x��
��2���⣺���ܣ�
��������y=4.88��
��4.88=-1.22x2+3.66x��
��x2-3x+4=0��
����-3��2-4��4��0��
���4.88=-1.22x2+3.66x�⣮
������ķ��и߶Ȳ��ܴﵽ4.88m��
��3���⣺��y=2.44��
��2.44=-1.22x2+3.66x��
��x2-3x+2=0��
��x1=1���������⣬��ȥ����x2=2��
����������߿�12m��������Ա����Ҫ��2s�ڵ����ŵ���߿�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����MBC�͡�NCB����ABC����ǣ���O�ǡ�MBC�͡�NCB��ƽ���ߵĽ��㣬��O������ABC������.

(1)��֪��A��100������ô��BOC���ڶ��ٶȣ�
(2)�����BOC���A��ʲô������ϵ?��֤����IJ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C��ֱ��AB��DE֮���һ�㣬��ACD=90�㣬����������ʹ��AB��DE���ǣ�����
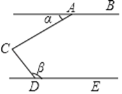
A. ����+����=180�� B. ����������=90�� C. ����=3���� D. ����+����=90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬABC�У���A=65������B=75��������C��DE���ۣ�ʹ��C������ABC��ĵ�![]() ��������1=20�������2�Ķ���Ϊ( )
��������1=20�������2�Ķ���Ϊ( )

A. 80��B. 90��
C. 100��D. 110��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������¥�IJ��ֽ��漰���������ͼ��С���ڼ�¥A��������E������¥F�����ֻ��֣���ʱA,E,F��ͬһֱ����.�ܵ�һ¥ʱ������Ա���ڽ�����ˮ���ˮ��·�߳������ߣ���1.2m�ߵ�D�������ˮ�����þ���E,F. ����B�͵�E����C��F����ظ߶ȷֱ���ͬ��������Ա��ˮ������������ƽ��0.4m�������������____m��ǡ�ð�ˮ�絽F���������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��PΪ������y=x2+2x��3�ڵ�һ�����ڵ�һ�����㣬��P����ԭ��ĶԳƵ�P��ǡ��Ҳ���ڸ��������ϣ����P��������Ϊ��������
A. ����1����1�� B. ����2����![]() �� C. ����
�� C. ����![]() ����2
����2![]() ��1�� D. ����
��1�� D. ����![]() ����2
����2![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����ij����һ���Ź��ŵĽ���ͼ�������Ŷ���������������״�����������˵���ˮ��ľ��붼��1m�����ŵĿ��Ϊ10m���Ŷ���ˮ�����������5m���Ŷ�������ϸ���һյ����ˮ��4m�ľ��۵ƣ��ְѹ��ŵĽ���ͼ����ƽ��ֱ������ϵ�У���ͼ��2����


��1�������ߵĽ���ʽ��
��2����յ���۵�P1��P2֮���ˮƽ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�������ε����߷ֱ���3��13m��8.

(1)��m��ȡֵ��Χ��
(2)�Ƿ��������mʹ�����ε��ܳ�Ϊż��?�����ڣ���������ε��ܳ����������ڣ�˵�����ɣ�
(3)��ͼ,��(2)��������,��AB=8,AC=13m,BC=3ʱ,��D��AB���е�,��CD,P��CD�϶���(����C,D�غ�,��P���߶�CD���˶�ʱ,������ʽ��):��![]() ;��
;��![]() ��������һ����ֵ���䣬��һ����ֵ�ı䡣���⣺
��������һ����ֵ���䣬��һ����ֵ�ı䡣���⣺
A.���жϳ�˭���䣬˭�ı䣻
B.������������ֵ�����ı������仯�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⷽ����
��1�����䷽���ⷽ�̣�x2��2x��1=0��
��2���ⷽ�̣�2x2+3x��1=0��
��3���ⷽ�̣�x2��4=3��x+2����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com