【题目】如图（1）是某河上一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状，抛物线两端点与水面的距离都是1m，拱桥的跨度为10m，桥洞与水面的最大距离是5m，桥洞两侧壁上各有一盏距离水面4m的景观灯．现把拱桥的截面图放在平面直角坐标系中，如图（2）．
求（1）抛物线的解析式；
（2）两盏景观灯P1、P2之间的水平距离.
科目：初中数学 来源： 题型：
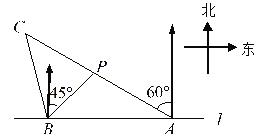
【题目】如图，在一笔直的海岸线
上有
、
两个观测站，在的正东方向，
（单位：
）有一艘小船在点
处，从测得小船在北偏西
的方向，从测得小船在北偏东
的方向．（结果保留根号）
（1）求点到海岸线的距离；
（2）小船从点处沿射线
的方向航行一段时间后，到达点
处，此时，从测得小船在北偏西
的方向，求点与点之间的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】每年的
月
日为世界环保日，为了提倡低碳环保，某公司决定购买
台节省能源的新设备，现有甲、乙两种型号的设备可供选购.经调查：购买
台甲型设备比购买
台乙型设备多花
万元，购买台甲型设备比购买台乙型设备少花万元.
（1）求甲、乙两种型号设备每台的价格；
（2）该公司经决定购买甲型设备不少于台，预算购买节省能源的新设备资金不超过
万元，你认为该公司有哪几种购买方案；
（3）在（2）的条件下，已知甲型设备每月的产量为
吨，乙型设备每月的产量为
吨.若每月要求产量不低于
吨，为了节约资金，请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一副三角板
和
拼合在一起，边
与
重合，
，
，
，
．当点
从点
出发沿向下滑动时，点
同时从点
出发沿射线
向右滑动．当点从点滑动到点时，连接
，则
的面积最大值为_______
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图①，正方形
的两边分别在正方形
的边
和
上，连接
．填空：线段
与的数量关系为________；直线与所夹锐角的大小为________．
（2）如图②，将正方形绕点
顺时针旋转，在旋转的过程中，（1）中的结论是否仍然成立，请说明理由．
（3）把图②中的正方形都换成菱形，且
，如图③，直接写出
______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）请用直尺、圆规作图，不写作法，但要保留作图痕迹．
已知：如图，∠ABC，射线BC上一点D．
求作：等腰△PBD，使线段BD为等腰△PBD的底边，点P在∠ABC内部，且点P到∠ABC两边的距离相等；
（2）在（1）的条件下，若∠ABC＝60°，求等腰三角形△PBD顶角的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料：
小明遇到这样一个问题：如图1,在△ABC中,DE∥BC分别交AB于D，交AC于E． 已知CD⊥BE，CD=3，BE=5，求BC+DE的值．
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2)．
（1）求证：DE=CF
（2）求BC+DE的值
（3）参考小明思考问题的方法，解决问题：
如图3，已知ABCD和矩形ABEF，AC与DF交于点G，AC=BF=DF，求∠AGF的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某企业新增了一个化工项目，为了节约资源，保护环境，该企业决定购买A、B两种型号的污水处理设备共8台，具体情况如下表：
经预算，企业最多支出89万元购买设备，且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱，说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
