
【题目】如图,设一个三角形的三边分别是3,13m,8.

(1)求m的取值范围;
(2)是否存在整数m使三角形的周长为偶数?若存在,求出三角形的周长;若不存在,说明理由;
(3)如图,在(2)的条件下,当AB=8,AC=13m,BC=3时,若D是AB的中点,连CD,P是CD上动点(不与C,D重合,当P在线段CD上运动时,有两个式子):①![]() ;②
;②![]() ,其中有一个的值不变,另一个的值改变。问题:
,其中有一个的值不变,另一个的值改变。问题:
A.请判断出谁不变,谁改变;
B.若不变的求出其值,若改变的求出变化的范围。
【答案】(1)![]() ;(2) 存在,理由见解析;(3) ①不改变,②改变,
;(2) 存在,理由见解析;(3) ①不改变,②改变,![]()
【解析】
(1) 根据三角形的三边关系即可求得;
(2)由(1)求得的 m取值范围,取整数,通过计算可得;
(3)利用等底等高的两个三角形面积相等以及三角形两边之和大于第三边的性质,通过计算可以求得答案.
(1)由三角形三边关系可得![]() ,解得
,解得![]() ;
;
(2)存在,理由是:
∵![]() ;
;
∴![]() 为整数的时候取值可为-3或-2,
为整数的时候取值可为-3或-2,
当![]() 时,
时,![]()
∴周长是3+8+10=21,不是偶数;
当![]() 时,
时,![]()
∴周长是![]() ,是偶数,所以存在.
,是偶数,所以存在.
(3)∵点D是AB的中点,则CD是中线,设点A到CD的距离为h,则点B到CD的距离也为h,
∴![]() ,
,![]()
![]() ,
,
∴![]() =
=![]() ,
,
∵![]() =
=![]() ,
,
∴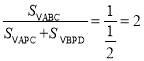
∴①不改变;
∵![]()
∴由三角形两边之和大于第三边性质可以知道![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() .
.
∴②改变.


科目:初中数学 来源: 题型:
【题目】国庆假期期间,某单位8名领导和320名员工集体外出进行素质拓展活动,准备租用45座大车或30座小车.若租用2辆大车3辆小车共需租车费1700元;若租用3辆大车2辆小车共需租车费1800元
(1)求大、小车每辆的租车费各是多少元?
(2)若每辆车上至少要有一名领导,每个人均有座位,且总租车费用不超过3100元,求最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球比赛中,某运动员将在地面上的足球对着球门踢出,图中的抛物线是足球的飞行高度y(m)关于飞行时间x(s)的函数图象(不考虑其它因素),已知足球飞出1s时,足球的飞行高度是2.44m,足球从飞出到落地共用3s.

(1)求y关于x的函数解析式;
(2)足球的飞行高度能否达到4.88 m?请说明理由;
(3)假设没有拦挡,足球将擦着球门左上角射入球门,球门的高为2.44 m(如图所示,足球的大小忽略不计).如果为了能及时将足球扑出,那么足球被踢出时,离球门左边框12m处的守门员至少要在几s内到球门的左边框?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
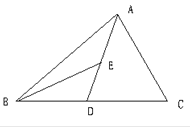
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 、
、![]() ,点
,点![]() 坐标为
坐标为![]() .
.
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 抛物线的顶点为
抛物线的顶点为![]() ,在
,在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 最小,并求出点
最小,并求出点![]() 的坐标;
的坐标;
![]() 点
点![]() 是线段
是线段![]() 上的动点,过点
上的动点,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .当
.当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
![]() 若平行于
若平行于![]() 轴的动直线
轴的动直线![]() 与该抛物线交于点
与该抛物线交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() .问:是否存在这样的直线
.问:是否存在这样的直线![]() ,使得
,使得![]() 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
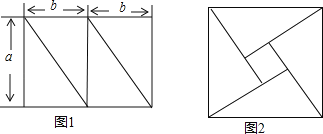
【题目】已知将边长分别为a和2b(a>b)的长方形分割成四个全等的直角三角形,如图1,再用这四个三角形拼成如图2所示的正方形,中间形成一个正方形的空洞.经测量得长方形的面积为24,正方形的边长为5.试通过你获取的信息,求a2+b2和a2﹣b2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列问题:
(1)若 n(n≠0)是关于 ![]() 的方程 x+mx-2n=0的根,求 m+n的值;
的方程 x+mx-2n=0的根,求 m+n的值;
(2)已知 ![]() ,
, ![]() 为实数,且 y=2
为实数,且 y=2![]() ,求 2x-3y的值.
,求 2x-3y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
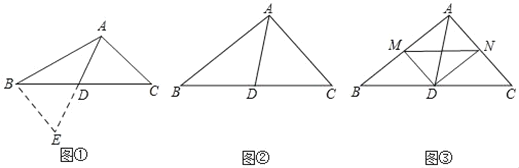
【题目】(问题情境)如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
(1)(问题解决)延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形三边的关系即可判断出中线AD的取值范围是 .
(反思感悟)解题时,条件中若出现“中点”、“中线”字样,可以考虑构造以该中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同个三角形中,从而解决问题.
(2)(尝试应用)如图②,△ABC中,∠BAC=90°,AD是BC边上的中线,试猜想线段AB,AC,AD之间的数量关系,并说明理由.
(3)(拓展延伸)如图③,△ABC中,∠BAC=90°,D是BC的中点,DM⊥DN,DM交AB于点M,DN交AC于点N,连接MN.当BM=4,MN=5,AC=6时,请直接写出中线AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com