
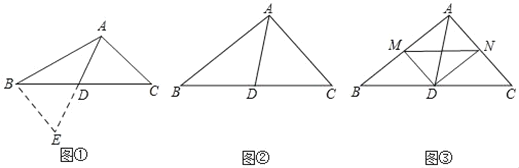
ЁОЬтФПЁПЃЈЮЪЬтЧщОГЃЉШчЭМЂйЃЌдкЁїABCжаЃЌШєAB=10ЃЌAC=6ЃЌЧѓBCБпЩЯЕФжаЯпADЕФШЁжЕЗЖЮЇЃЎ
ЃЈ1ЃЉЃЈЮЪЬтНтОіЃЉбгГЄADЕНЕуEЪЙDE=ADЃЌдйСЌНгBEЃЈЛђНЋЁїACDШЦзХЕуDФцЪБеыа§зЊ180ЁуЕУЕНЁїEBDЃЉЃЌАбABЁЂACЁЂ2ADМЏжадкЁїABEжаЃЌРћгУШ§НЧаЮШ§БпЕФЙиЯЕМДПЩХаЖЯГіжаЯпADЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЎ
ЃЈЗДЫМИаЮђЃЉНтЬтЪБЃЌЬѕМўжаШєГіЯжЁАжаЕуЁБЁЂЁАжаЯпЁБзжбљЃЌПЩвдПМТЧЙЙдьвдИУжаЕуЮЊЖдГЦжааФЕФжааФЖдГЦЭМаЮЃЌАбЗжЩЂЕФвбжЊЬѕМўКЭЫљЧѓжЄЕФНсТлМЏжаЕНЭЌИіШ§НЧаЮжаЃЌДгЖјНтОіЮЪЬтЃЎ
ЃЈ2ЃЉЃЈГЂЪдгІгУЃЉШчЭМЂкЃЌЁїABCжаЃЌЁЯBAC=90ЁуЃЌADЪЧBCБпЩЯЕФжаЯпЃЌЪдВТЯыЯпЖЮABЃЌACЃЌADжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ3ЃЉЃЈЭиеЙбгЩьЃЉШчЭМЂлЃЌЁїABCжаЃЌЁЯBAC=90ЁуЃЌDЪЧBCЕФжаЕуЃЌDMЁЭDNЃЌDMНЛABгкЕуMЃЌDNНЛACгкЕуNЃЌСЌНгMNЃЎЕБBM=4ЃЌMN=5ЃЌAC=6ЪБЃЌЧыжБНгаДГіжаЯпADЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2ЃМADЃМ8ЃЛЃЈ2ЃЉAB2ЃЋAC2ЃН4AD2ЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉADЃН5ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉбгГЄADжСEЃЌЪЙDEЃНADЃЌгЩSASжЄУїЁїBDEЁеЁїCDAЃЌЕУГіBEЃНACЃН8ЃЌдкЁїABEжаЃЌгЩШ§НЧаЮЕФШ§БпЙиЯЕЧѓГіAEЕФШЁжЕЗЖЮЇЃЌМДПЩЕУГіADЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉбгГЄADжСEЃЌЪЙDEЃНADЃЌСЌНгBEЃЌШчЭМЂкЫљЪОЃЌгЩЃЈ1ЃЉПЩжЊЁїBDEЁеЁїCDAЃЌШЛКѓжЛвЊжЄУїЁЯABEЃН90ЁуЃЌРћгУЙДЙЩЖЈРэМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉбгГЄNDЕНEЃЌЪЙЕУDNЃНDEЃЌСЌНгBEЁЂEMЃЌЪзЯШжЄУїЁїBDEЁеЁїCDNЃЌЧѓГіЁЯABDЃЋЁЯDBEЃН90ЁуЃЌШЛКѓРћгУЙДЙЩЖЈРэПЩЕУBEЃН3ЃЌНјЖјЕУЕНANЃНNCЃЌРћгУШ§ЯпКЯвЛжЄУїDNЁЭACЃЌЭЌРэПЩЕУDMЁЭABЃЌШЛКѓжЄУїЫФБпаЮAMDNЪЧОиаЮМДПЩНтОіЮЪЬт.
НтЃКЃЈ1ЃЉбгГЄADжСEЃЌЪЙDEЃНADЃЌСЌНгBEЃЌШчЭМЂйЫљЪОЃЌ
ЁпADЪЧBCБпЩЯЕФжаЯпЃЌ
ЁрBDЃНCDЃЌ
дкЁїBDEКЭЁїCDAжаЃЌ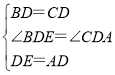 ЃЌ
ЃЌ
ЁрЁїBDEЁеЁїCDAЃЈSASЃЉЃЌ
ЁрBEЃНACЃН6ЃЌ
дкЁїABEжаЃЌгЩШ§НЧаЮЕФШ§БпЙиЯЕЕУЃКABBEЃМAEЃМABЃЋBEЃЌ
Ёр106ЃМAEЃМ10ЃЋ6ЃЌМД4ЃМAEЃМ16ЃЌ
Ёр2ЃМADЃМ8ЃЛ
ЃЈ2ЃЉAB2ЃЋAC2ЃН4AD2ЃЌ
РэгЩЃКбгГЄADжСEЃЌЪЙDEЃНADЃЌСЌНгBEЃЌШчЭМЂкЫљЪОЃЌ
гЩЃЈ1ЃЉПЩжЊЃКЁїBDEЁеЁїCDAЃЌ
ЁрBEЃНACЃЌЁЯEЃНЁЯCADЃЌ
ЁпЁЯBACЃН90ЁуЃЌ
ЁрЁЯEЃЋЁЯBAEЃНЁЯBAEЃЋЁЯCADЃНЁЯBACЃН90ЁуЃЌ
ЁрЁЯABEЃН90ЁуЃЌ
ЁрAB2ЃЋBE2ЃНAE2ЃЌ
ЁрAB2ЃЋAC2ЃН4AD2ЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌбгГЄNDЕНEЃЌЪЙЕУDNЃНDEЃЌСЌНгBEЁЂEMЃЎ

ЁпBDЃНDCЃЌЁЯBDEЃНЁЯCDNЃЌDEЃНDNЃЌ
ЁрЁїBDEЁеЁїCDNЃЌ
ЁрBEЃНCMЃЌЁЯEBDЃНЁЯCЃЌ
ЁпЁЯABCЃЋЁЯCЃН90ЁуЃЌ
ЁрЁЯABDЃЋЁЯDBEЃН90ЁуЃЌ
ЁпMDЁЭENЃЌDEЃНDNЃЌ
ЁрMEЃНMNЃН5ЃЌ
дкRtЁїBEMжаЃЌBEЃН![]() ЃН3ЃЌ
ЃН3ЃЌ
ЁрCNЃНBEЃН3ЃЌ
ЁпACЃН6ЃЌ
ЁрANЃНNCЃЌ
ЁпЁЯBACЃН90ЁуЃЌBDЃНDCЃЌ
ЁрADЃНDCЃНBDЃЌ
ЁрDNЁЭACЃЌ
дкRtЁїAMNжаЃЌAMЃН![]() ЃН4ЃЌ
ЃН4ЃЌ
ЁрAMЃНBMЃЌ
ЁпDAЃНDBЃЌ
ЁрDMЁЭABЃЌ
ЁрЁЯAMDЃНЁЯANDЃНЁЯMANЃН90ЁуЃЌ
ЁрЫФБпаЮAMDNЪЧОиаЮЃЌ
ЁрADЃНMNЃН5ЃЎ


 вЛБОКУЬтПкЫуЬтПЈЯЕСаД№АИ
вЛБОКУЬтПкЫуЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЩшвЛИіШ§НЧаЮЕФШ§БпЗжБ№ЪЧ3ЃЌ13mЃЌ8.

(1)ЧѓmЕФШЁжЕЗЖЮЇЃЛ
(2)ЪЧЗёДцдкећЪ§mЪЙШ§НЧаЮЕФжмГЄЮЊХМЪ§?ШєДцдкЃЌЧѓГіШ§НЧаЮЕФжмГЄЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
(3)ШчЭМ,дк(2)ЕФЬѕМўЯТ,ЕБAB=8,AC=13m,BC=3ЪБ,ШєDЪЧABЕФжаЕу,СЌCD,PЪЧCDЩЯЖЏЕу(ВЛгыC,DжиКЯ,ЕБPдкЯпЖЮCDЩЯдЫЖЏЪБ,гаСНИіЪНзг):Ђй![]() ;Ђк
;Ђк![]() ЃЌЦфжагавЛИіЕФжЕВЛБфЃЌСэвЛИіЕФжЕИФБфЁЃЮЪЬтЃК
ЃЌЦфжагавЛИіЕФжЕВЛБфЃЌСэвЛИіЕФжЕИФБфЁЃЮЪЬтЃК
A.ЧыХаЖЯГіЫВЛБфЃЌЫИФБфЃЛ
B.ШєВЛБфЕФЧѓГіЦфжЕЃЌШєИФБфЕФЧѓГіБфЛЏЕФЗЖЮЇЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтЗНГЬЃК
ЃЈ1ЃЉгУХфЗНЗЈНтЗНГЬЃКx2Љ2xЉ1=0ЃЎ
ЃЈ2ЃЉНтЗНГЬЃК2x2+3xЉ1=0ЃЎ
ЃЈ3ЃЉНтЗНГЬЃКx2Љ4=3ЃЈx+2ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуAЃЌBдкЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯЃЌЕуCЃЌDдкЗДБШР§КЏЪ§
ЕФЭМЯѓЩЯЃЌЕуCЃЌDдкЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯЃЌAC//BD//yжсЃЌвбжЊЕуAЃЌBЕФКсзјБъЗжБ№ЮЊ1ЃЌ2ЃЌЁїOACгыЁїABDЕФУцЛ§жЎКЭЮЊ
ЕФЭМЯѓЩЯЃЌAC//BD//yжсЃЌвбжЊЕуAЃЌBЕФКсзјБъЗжБ№ЮЊ1ЃЌ2ЃЌЁїOACгыЁїABDЕФУцЛ§жЎКЭЮЊ![]() ЃЌдђkЕФжЕЮЊЃЈ ЃЉ
ЃЌдђkЕФжЕЮЊЃЈ ЃЉ

A. 4 B. 3 C. 2 D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌОиаЮOABCЕФБпгыКЏЪ§y=![]() ЃЈxЃО0ЃЉЭМЯѓНЛгкEЃЌFСНЕуЃЌЧвFЪЧBCЕФжаЕуЃЌдђЫФБпаЮACFEЕФУцЛ§ЕШгкЃЈЁЁЁЁЃЉ
ЃЈxЃО0ЃЉЭМЯѓНЛгкEЃЌFСНЕуЃЌЧвFЪЧBCЕФжаЕуЃЌдђЫФБпаЮACFEЕФУцЛ§ЕШгкЃЈЁЁЁЁЃЉ
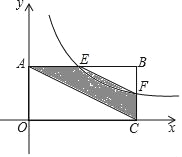
A. 4 B. 6 C. 8 D. ВЛФмШЗЖЈ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаДгзѓБпЕНгвБпЕФБфаЮЃЌЪЧвђЪНЗжНтЕФЪЧЃЈЁЁЁЁЃЉ
A.y![]() Љ5yЉ6ЃНЃЈyЉ6ЃЉЃЈy+1ЃЉB.a
Љ5yЉ6ЃНЃЈyЉ6ЃЉЃЈy+1ЃЉB.a![]() +4aЉ3ЃНaЃЈa+4ЃЉЉ3
+4aЉ3ЃНaЃЈa+4ЃЉЉ3
C.xЃЈxЉ1ЃЉЃНx![]() ЉxD.m
ЉxD.m![]() +n
+n![]() ЃНЃЈm+nЃЉЃЈmЉnЃЉ
ЃНЃЈm+nЃЉЃЈmЉnЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§y=x+![]() ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎ
ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁУїЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉКЏЪ§y=x+![]() ЕФздБфСПxЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
ЕФздБфСПxЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
ЃЈ2ЃЉЯТБэСаГіСЫyгыxЕФМИзщЖдгІжЕЃЌЧыаДГіmЃЌnЕФжЕЃКm=_____ЃЌn=_____ЃЛ
x | Ё | Љ3 | Љ2 | Љ1 | Љ | Љ |
|
| 1 | 2 | 3 | 4 | Ё |
y | Ё | Љ | Љ | Љ2 | Љ | Љ | m |
| 2 |
| n |
| Ё |
ЃЈ3ЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌУшГіСЫвдЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌИљОнУшГіЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ4ЃЉНсКЯКЏЪ§ЕФЭМЯѓЃЌЧыЭъГЩЃК
ЂйЕБy=Љ![]() ЪБЃЌx=_____ЃЎ
ЪБЃЌx=_____ЃЎ
ЂкаДГіИУКЏЪ§ЕФвЛЬѕаджЪ_____ЃЎ
ЂлШєЗНГЬx+![]() =tгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌдђtЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
=tгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌдђtЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋвЛИБШ§НЧГпАДШчЭМЂйЗНЪНЦДНгЃККЌ30ЁуНЧЕФШ§НЧГпЕФГЄжБНЧБпгыКЌ45ЁуНЧЕФШ§НЧГпЕФаББпЧЁКУжиКЯЃЈдкRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌЁЯBACЃН30ЁуЃЛдкRtЁїACDжаЃЌЁЯADCЃН90ЁуЁЯDACЃН45ЁуЃЉвбжЊABЃН2![]() ЃЌPЪЧACЩЯЕФвЛИіЖЏЕуЃЎ
ЃЌPЪЧACЩЯЕФвЛИіЖЏЕуЃЎ

ЃЈ1ЃЉЕБPDЃНBCЪБЃЌЧѓЁЯPDAЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌШєEЪЧCDЕФжаЕуЃЌЧѓЁїDEPжмГЄЕФзюаЁжЕЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌЕБDPЦНЗжЁЯADCЪБЃЌдкЁїABCФкДцдквЛЕуQЃЌЪЙЕУЁЯDQCЃНЁЯDPCЃЌЧвCQЃН![]() ЃЌЧѓPQЕФГЄЃЎ
ЃЌЧѓPQЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ9ЗжЃЉФГХњЗЂЩЬвдУПМў50дЊЕФМлИёЙКНј800МўTаєЃЌЕквЛИідТвдЕЅМл80дЊЯњЪлЃЌЪлГіСЫ200МўЃЛЕкЖўИідТШчЙћЕЅМлВЛБфЃЌдЄМЦШдПЩЪлГі200МўЃЌХњЗЂЩЬЮЊдіМгЯњЪлСПЃЌОіЖЈНЕМлЯњЪлЃЌИљОнЪаГЁЕїВщЃЌЕЅМлУПНЕЕЭ1дЊЃЌПЩЖрЪлГі10МўЃЌЕЋзюЕЭЕЅМлгІИпгкЙКНјЕФМлИёЃЛЕкЖўИідТНсЪјКѓЃЌХњЗЂЩЬНЋЖдЪЃгрЕФTаєвЛДЮадЧхВжЯњЪлЃЌЧхВжЪЧЕЅМлЮЊ40дЊЃЌЩшЕкЖўИідТЕЅМлНЕЕЭ![]() дЊЃЎ
дЊЃЎ
ЃЈ1ЃЉЬюБэЃКЃЈВЛашЛЏМђЃЉ

ЃЈ2ЃЉШчЙћХњЗЂЩЬЯЃЭћЭЈЙ§ЯњЪлетХњTаєЛёРћ9000дЊЃЌФЧУДЕкЖўИідТЕФЕЅМлгІЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com