
【题目】如图,平面直角坐标系中,矩形OABC的边与函数y=![]() (x>0)图象交于E,F两点,且F是BC的中点,则四边形ACFE的面积等于( )
(x>0)图象交于E,F两点,且F是BC的中点,则四边形ACFE的面积等于( )
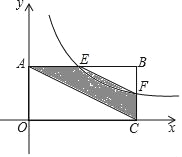
A. 4 B. 6 C. 8 D. 不能确定
【答案】B
【解析】
由四边形OABC是矩形,F是BC的中点,可设F(m,n),则B(m,2n),又E点在抛物线上,则E(![]() ,2n).可以用含m,n的式子表示出矩形OABC,三角形AOC和三角形BEF的面积.F在反比例函数的图形上可得到mn的关系,
,2n).可以用含m,n的式子表示出矩形OABC,三角形AOC和三角形BEF的面积.F在反比例函数的图形上可得到mn的关系,
再依据S四边形ACFE =S矩形OABC-S△AOC-S△BEF.即可求.
解:∵边形OABC是矩形,F是BC的中点,
∴可设F(m,n),则B(m,2n),又E点在抛物线上,则E(![]() ,2n),
,2n),
∵F在抛物线上,
∴mn=8,
∵F(m,n),B(m,2n), E(![]() ,2n),
,2n),
∴OA=2n,AB=OC=m,AE=![]() ,BF=n,
,BF=n,
∴S矩形OABC=2mn,
S△AOC =![]() ×OA×OC==
×OA×OC==![]() ×2n×m=mn,
×2n×m=mn,
S△BEF =![]() ×BE×BF=
×BE×BF=![]() ×(m-
×(m-![]() )×n=
)×n=![]() mn-4,
mn-4,
∵S四边形ACFE =S矩形OABC-S△AOC-S△BEF,
∴S四边形ACFE =2mn-mn-(![]() mn-4)=
mn-4)=![]() mn+2,
mn+2,
∵mn=8,
∴S四边形ACFE =![]() mn+2=6.
mn+2=6.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
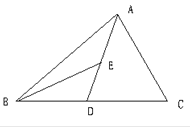
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的大小;
(2)若CD=3,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
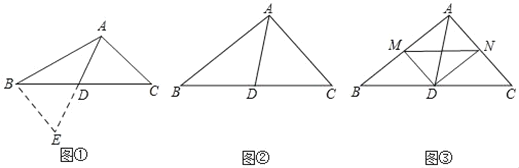
【题目】(问题情境)如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
(1)(问题解决)延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形三边的关系即可判断出中线AD的取值范围是 .
(反思感悟)解题时,条件中若出现“中点”、“中线”字样,可以考虑构造以该中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同个三角形中,从而解决问题.
(2)(尝试应用)如图②,△ABC中,∠BAC=90°,AD是BC边上的中线,试猜想线段AB,AC,AD之间的数量关系,并说明理由.
(3)(拓展延伸)如图③,△ABC中,∠BAC=90°,D是BC的中点,DM⊥DN,DM交AB于点M,DN交AC于点N,连接MN.当BM=4,MN=5,AC=6时,请直接写出中线AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
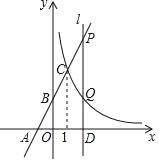
【题目】如图,直线y=kx+2与x轴,y轴分别交于点A(﹣1,0)和点B,与反比例函数y=![]() 的图象在第一象限内交于点C(1,n).
的图象在第一象限内交于点C(1,n).
(1)求一次函数y=kx+2与反比例函数y=![]() 的表达式;
的表达式;
(2)过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线y=kx+2和双曲线y=![]() 交于P、Q两点,且PQ=2QD,求点D的坐标.
交于P、Q两点,且PQ=2QD,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,AB=4,点E,F在对角线BD上,AE∥CF.
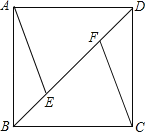
(1)求证:△ABE≌△CDF;
(2)若∠ABE=2∠BAE,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一,下列图表中的数据是运动员甲、乙、丙三人每人10次垫球测试的成绩,测试规则为每次连续接球10个,每垫球到位1个记1分,已知运动员甲测试成绩的中位数和众数都是7.
运动员甲测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 |
| 6 | 8 | 6 | 8 |
|
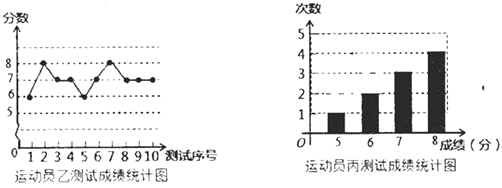
(1)填空:![]() ______;
______;![]() ______.
______.
(2)要从他们三人中选择一位垫球较为稳定的接球能手,你认为选谁更合适?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com