【题目】已知点P为抛物线y=x2+2x﹣3在第一象限内的一个动点，且P关于原点的对称点P′恰好也落在该抛物线上，则点P′的坐标为（ ）
A. （﹣1，﹣1） B. （﹣2，﹣
） C. （﹣
，﹣2﹣1） D. （﹣，﹣2）
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】某商场计划购进一批甲、乙两种玩具，已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元，用90元购进甲种玩具的件数与用150元购进的乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件，购进这两种玩具的总资金超过960元但不超过1000元，求商场有哪几种具体的进货方案?最多可以购进乙种玩具多少件?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】足球比赛中，某运动员将在地面上的足球对着球门踢出，图中的抛物线是足球的飞行高度y（m）关于飞行时间x（s）的函数图象（不考虑其它因素），已知足球飞出1s时，足球的飞行高度是2.44m，足球从飞出到落地共用3s．
（1）求y关于x的函数解析式；
（2）足球的飞行高度能否达到4.88 m？请说明理由；
（3）假设没有拦挡，足球将擦着球门左上角射入球门，球门的高为2.44 m（如图所示，足球的大小忽略不计）．如果为了能及时将足球扑出，那么足球被踢出时，离球门左边框12m处的守门员至少要在几s内到球门的左边框？
查看答案和解析>>
科目：初中数学 来源： 题型：
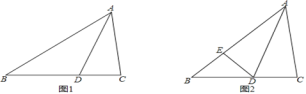
【题目】在△ABC中，AD是它的角平分线．
（1）如图1，求证：S△ABD：S△ACD＝AB：AC＝BD：CD；
（2）如图2，E是AB上的点，连接ED，若BD＝3，BE＝CD＝2，AE＝2CD，求证：△BED是等腰三角形；
（3）在图1中，若3∠BAC＝2∠C，∠ADB＞∠B＞∠BAD，直接写出∠BAC的取值范围 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某景区内有一块矩形油菜花田地（数据如图示，单位：m.）现在其中修建一条观花道（图中阴影部分）供游人赏花.设改造后剩余油菜花地所占面积为ym2.
（1）求y与x的函数表达式；
（2）若改造后观花道的面积为13m2，求x的值；
（3）若要求 0.5≤ x ≤1，求改造后剩余油菜花地所占面积的最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
与
轴交于点
，与
轴交于点
、
，点坐标为
．
求该抛物线的解析式；
抛物线的顶点为
，在轴上找一点
，使
最小，并求出点的坐标；
点
是线段
上的动点，过点作
，交
于点
，连接
．当
的面积最大时，求点的坐标；
若平行于轴的动直线
与该抛物线交于点
，与直线
交于点
，点
的坐标为
．问：是否存在这样的直线，使得
是等腰三角形？若存在，请求出点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数y＝
(k≠0)在第一象限的图象经过顶点A(m，2)和CD边上的点E(n，
)，过点E的直线l交x轴于点F，交y轴于点G(0，－2)，则点F的坐标是( )
A. (
，0)B. (
，0)C. (
，0)D. (
，0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
