
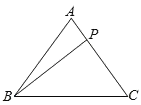
【题目】△ABC中,有一点P在AC上移动.若AB=AC=5,BC=6,AP+BP+CP的最小值为_____.
【答案】9.8.
【解析】
若AP+BP+CP最小,就是说当BP最小时,AP+BP+CP才最小,因为不论点P在AC上的那一点,AP+CP都等于AC.那么就需从B向AC作垂线段,交AC于P.先设AP=x,再利用勾股定理可得关于x的方程,解即可求x,在Rt△ABP中,利用勾股定理可求BP.那么AP+BP+CP的最小值可求.
解:从B向AC作垂线段BP,交AC于P,
设AP=x,则CP=5﹣x,
在Rt△ABP中,BP2=AB2﹣AP2,
在Rt△BCP中,BP2=BC2﹣CP2,
∴AB2﹣AP2=BC2﹣CP2,
∴52﹣x2=62﹣(5﹣x)2
解得x=1.4,
在Rt△ABP中,BP=![]() =
=![]() =4.8,
=4.8,
∴AP+BP+CP=AC+BP=5+4.8=9.8.
故答案为:9.8.


科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
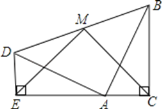
【题目】两个全等的含30°,60°角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.试判断△EMC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
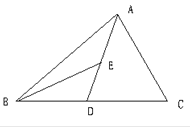
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
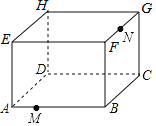
【题目】如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为( )
A.20cmB.2![]() cmC.(12+2
cmC.(12+2![]() )cmD.18cm
)cmD.18cm
查看答案和解析>>
科目:初中数学 来源: 题型:
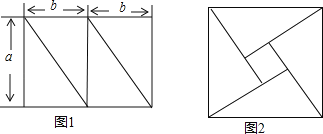
【题目】已知将边长分别为a和2b(a>b)的长方形分割成四个全等的直角三角形,如图1,再用这四个三角形拼成如图2所示的正方形,中间形成一个正方形的空洞.经测量得长方形的面积为24,正方形的边长为5.试通过你获取的信息,求a2+b2和a2﹣b2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.

(1)若∠A=60°,求BC的长;
(2)若sinA=![]() ,求AD的长.
,求AD的长.
(注意:本题中的计算过程和结果均保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的大小;
(2)若CD=3,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
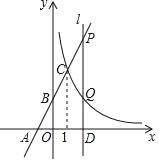
【题目】如图,直线y=kx+2与x轴,y轴分别交于点A(﹣1,0)和点B,与反比例函数y=![]() 的图象在第一象限内交于点C(1,n).
的图象在第一象限内交于点C(1,n).
(1)求一次函数y=kx+2与反比例函数y=![]() 的表达式;
的表达式;
(2)过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线y=kx+2和双曲线y=![]() 交于P、Q两点,且PQ=2QD,求点D的坐标.
交于P、Q两点,且PQ=2QD,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com