
【题目】如图,在直角坐标系中,A(-a,0),B(b,0),C(0,c),且满足![]() .
.
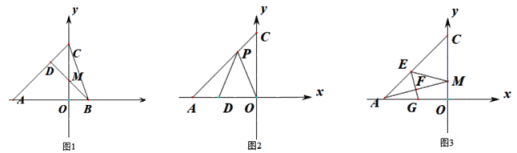
(1)如图1,过B作BD⊥AC,交y轴于M,垂足为D,求M点的坐标.
(2)如图2,若a=3![]() ,AC=6,点P为线段AC上一点,D为x轴负半轴上一点,且PD=PO,∠DPO=45°,求点D的坐标.
,AC=6,点P为线段AC上一点,D为x轴负半轴上一点,且PD=PO,∠DPO=45°,求点D的坐标.
(3)如图3,M在OC上,E在AC上,满足∠CME=∠OMA,EF⊥AM交AO于G,垂足为F,试猜想线段OG,OM,CM三者之间的数量关系,并给出证明.
【答案】(1)M(0,2);(2)D(![]() ,0);(3)OG+OM=CM,证明见解析.
,0);(3)OG+OM=CM,证明见解析.
【解析】
(1)由被开方数大于等于0,可得a=c,b=2,则B点坐标为(2,0),易得△OAC和△OBM为等腰直角三角形,所以OM=OB=2,从而得到M点坐标;
(2)由“一线三等角”模型,易证△PAD≌△OCP,从而得到AP=OC,AD=PC,即可求出OD的长度,进而得到D点坐标;
(3)设OM=m,则M点坐标为(0,m),分别求出AC、AM、EM的解析式,将EM与AC联立求得E点坐标,再根据EF⊥AM,可得EF的斜率,进而求出EF的解析式,然后求出G点坐标即可得出关系.
解:(1)由题意得![]() ,
,
∴![]() ,
,![]()
∴OA=OC,B点坐标(2,0)
∴∠OAC=∠OCA=45°,
又∵BD⊥AC
∴∠OBM=45°,
∴∠OMB=∠OBM=45°,
∴OM=OB=2
∴M点的坐标为(0,2)
(2)∵∠APO=∠APD+∠DPO=∠PCO+∠POC,且∠DPO=∠PCO=45°
∴∠APD=∠POC
在△PAD和△OCP中,
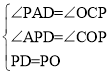
∴△PAD≌△OCP(AAS)
∴AP=OC=![]() ,AD=PC
,AD=PC
∴PC=AC-AP=![]() =AD
=AD
∴OD=OA-AD=![]()
∵D点在x轴负半轴,
∴D点坐标为(![]() ,0)
,0)
(3)OG+OM=CM,证明如下:
设OM=m,则M点坐标为(0,m)
由(1)可知OA=OC=a,A点坐标为(-a,0),C点坐标为(0,a)
∴AC直线解析式为:![]()
AM直线解析式为:![]()
如图,延长EM,AO交于点H,
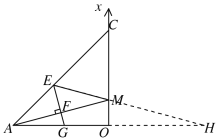
∵∠CME=∠OMA,∠CME=∠OMH
∴∠OMA=∠OMH
又∵MO⊥AH
∴OA=OH=a
∴直线EH解析式为:![]()
将直线AC与直线EH联立得
 解得
解得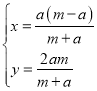
∴E点坐标为(![]() ,
,![]() )
)
∵EF⊥AM
∴kEF·kAM=-1
∴kEF=![]()
设EF解析式为: ![]()
将E点坐标(![]() ,
,![]() )代入得
)代入得
![]() =
=![]() ,解得
,解得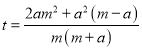
设EF解析式为: 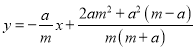
当y=0时,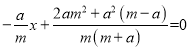
解得![]()
∴G点坐标为(![]() ,0)
,0)
∵G在x轴的负半轴
∴OG=![]()
∴OG+OM=![]()
又∵CM=OC-OM=![]()
∴OG+OM=CM


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 、
、![]() ,点
,点![]() 坐标为
坐标为![]() .
.
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 抛物线的顶点为
抛物线的顶点为![]() ,在
,在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 最小,并求出点
最小,并求出点![]() 的坐标;
的坐标;
![]() 点
点![]() 是线段
是线段![]() 上的动点,过点
上的动点,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .当
.当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
![]() 若平行于
若平行于![]() 轴的动直线
轴的动直线![]() 与该抛物线交于点
与该抛物线交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() .问:是否存在这样的直线
.问:是否存在这样的直线![]() ,使得
,使得![]() 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列问题:
(1)若 n(n≠0)是关于 ![]() 的方程 x+mx-2n=0的根,求 m+n的值;
的方程 x+mx-2n=0的根,求 m+n的值;
(2)已知 ![]() ,
, ![]() 为实数,且 y=2
为实数,且 y=2![]() ,求 2x-3y的值.
,求 2x-3y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=![]() (k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,
(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,![]() ),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是( )
),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是( )

A. (![]() ,0)B. (
,0)B. (![]() ,0)C. (
,0)C. (![]() ,0)D. (
,0)D. (![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=![]() 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=8,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=8,则k的值是( )

A. 3 B. 4 C. 5 D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程kx2-2(k+1)x+k-1=0有两个不相等的实数根x1,x2.
(1)求k的取值范围;
(2)是否存在实数k,使![]() =1成立?若存在,请求出k的值;若不存在,请说明理由.
=1成立?若存在,请求出k的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com