
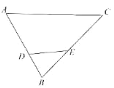
【题目】尺规作图(不用写出作法,保留作图痕迹):
(1)在 DE 的上方,求作![]() FDE,使得
FDE,使得![]() FDE≌
FDE≌![]() BDE;
BDE;
(2)若∠B=50°,则∠ADF+∠CEF= °.
科目:初中数学 来源: 题型:
【题目】下列说法中错误的是( )
A.平行四边形的对角线互相平分
B.有两对邻角互补的四边形为平行四边形
C.对角线互相平分的四边形是平行四边形
D.一组对边平行,一组对角相等的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了扩大经营,决定购进6台机器用于生产某活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(个) | 100 | 60 |
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择什么样的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个袋中有3张形状大小完全相同的卡片,编号为1,2,3,先任取一张,将其编号记为m,再从剩下的两张中任取一张,将其编号记为n.
(1)请用树状图或者列表法,表示事件发生的所有可能情况;
(2)求关于x的方程x2+mx+n=0有两个不相等实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
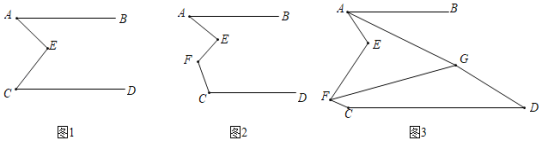
【题目】如图,AB∥CD.
(1)如图1,∠A、∠E、∠C的数量关系为 .
(2)如图2,若∠A=50°,∠F=115°,求∠C﹣∠E的度数;
(3)如图3,∠E=90°,AG,FG分别平分∠BAE,∠CFE,若GD∥FC,试探究∠AGF与∠GDC的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠BAC=90°,AB=AC.
(1)如图,D为AC上任一点,连接BD,过A点作BD的垂线交过C点与AB平行的直线CE于点E.求证:BD=AE.
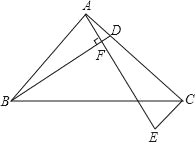
(2)若点D在AC的延长线上,如图,其他条件同(1),请画出此时的图形,并猜想BD与AE是否仍然相等?说明你的理由.
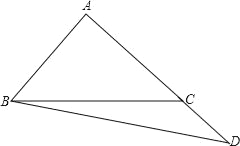
查看答案和解析>>
科目:初中数学 来源: 题型:
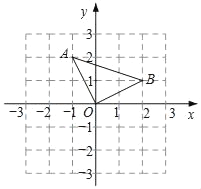
【题目】如图,在平面直角坐标系xOy中,点O(0,0),A(﹣1,2),B(2,1).
(1)在图中画出△AOB关于y轴对称的△A1OB1,并直接写出点A1和点B1的坐标;(不写画法,保留画图痕迹)
(2)在x轴上存在点P,使得PA+PB的值最小,则点P的坐标为 ,PA+PB的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.

(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.试探究ND,DG与AD数量之间的关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com