
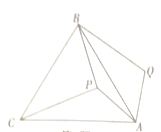
【题目】如图,![]() 是等边三角形
是等边三角形![]() 内一点,将线段
内一点,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
连结PQ,先根据等边三角形的性质和旋转的性质证明△APQ为等边三角形,则P Q=AP=6,再证明△APC≌△AQB,可得PC=QB=10,然后利用勾股定理的逆定理证明△PBQ为直角三角形,再根据三角形面积公式求出面积,最后利用S四边形APBQ=S△BPQ+S△APQ即可解答.
解:如图,连结PQ,
∵△ABC为等边三角形,
∴∠BAC=60°,AB=AC,
∵线段AP绕点A顺时针旋转60°得到线段AQ,
∴AP=PQ=6,∠PAQ=60°,
∴△APQ为等边三角形,
∴PQ=AP=6,
∵∠CAP+∠BAP=60°,∠BAP+∠BAQ=60°,
∴∠CAP=∠BAQ,
∵在△APC和△ABQ中,AC=AB,∠CAP=∠BAQ,AP=AQ
∴△APC≌△AQB,
∴PC=QB=10,
在△BPQ中, PB2=82=64,PQ2=62=36,BQ2=102=100,
∴PB2+PQ2=BQ2,
∴△PBQ为直角三角形,
∴∠BPQ=90°,
∴S四边形APBQ=S△BPQ+S△APQ=![]() ×6×8+
×6×8+![]() ×62=24+9
×62=24+9![]()
故答案为A..


科目:初中数学 来源: 题型:
【题目】阅读理解:
圆是最完美的图形,它具有一些特殊的性质:同弧或等弧所对的圆周角相等,一条弧所对的圆周角等于这条弧所对的圆心角的一半……;先构造“辅助圆”,再利用圆的性质将问题进行转化,往往能化隐为显、化难为易.

解决问题:
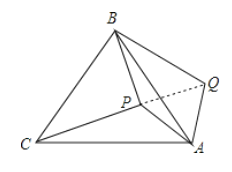
如图,点![]() 与点
与点![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,点
,点![]() 是该直角坐标系内的一个动点.
是该直角坐标系内的一个动点.
(1)使![]() 的点
的点![]() 有_________个;
有_________个;
(2)若点![]() 在
在![]() 的负半轴上,且
的负半轴上,且![]() ,求满足条件的点
,求满足条件的点![]() 的坐标;
的坐标;
(3)当![]() 为锐角时,设
为锐角时,设![]() ,若点
,若点![]() 在
在![]() 轴上移动时,满足条件的点
轴上移动时,满足条件的点![]() 有4个,求
有4个,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=![]() x+2与x轴交于点A,与y轴交于点C,抛物线y=
x+2与x轴交于点A,与y轴交于点C,抛物线y=![]() x2+bx+c经过A、C两点,与x轴的另一交点为点B.
x2+bx+c经过A、C两点,与x轴的另一交点为点B.

(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点;
①连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S1, △BCE的面积为S2, 求![]() 的最大值;
的最大值;
②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店销售学习用品,已知某品牌钢笔的进价是20元,销售过程发现,每月销量y支与销售单价x元(x为正整数)之间满足一次函数关系,且每支钢笔的售价不低于进价,也不高于35元,下表是y与x之间的对应数据:
销售单价x(元) | … | 22 | 24 | 30 | … |
月销量y(只) | … | 92 | 84 | 60 | … |
(1)求y与x的函数关系式并直接写出自变量x的取值范围.
(2)每支钢笔的售价定为多少元时,月销售利润恰为600元?
(3)每支钢笔的售价定为多少元时可使月销售利润最大?最大的月利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
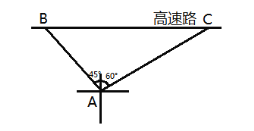
【题目】很多交通事故是由于超速行驶导致的,为集中治理超速现象,高速交警在距离高速路40米的地方设置了一个测速观察点,现测得测速点的西北方向有一辆小型轿车从B处沿西向正东方向行驶,2秒钟后到达测速点北偏东![]() 的方向上的C处,如图.
的方向上的C处,如图.
(1)求该小型轿车在测速过程中的平均行驶速度约是多少千米/时(精确到1千米/时)?
(参考数据:![]() )
)
(2)我国交通法规定:小轿车在高速路行驶,时速超过限定速度10%以上不到50%的处200元罚款,扣3分;时速超过限定速度50%以上不到70%的处1500元罚款,扣12分;时速超过限定时速70%以上的处1500元罚款,扣12分.若该高速路段限速120千米/时,你认为该小轿车驾驶员会受到怎样的处罚.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点.
边的中点.
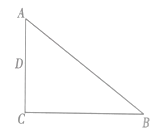
(1)尺规作图:作出以![]() 为直径的圆
为直径的圆![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .(保留作图痕迹,不写作法)
.(保留作图痕迹,不写作法)
(2)求证:![]() 是圆
是圆![]() 的切线.
的切线.
(3)当![]() 时,四边形
时,四边形![]() 是平行四边形,此时,四边形
是平行四边形,此时,四边形![]() 的形状为 .
的形状为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
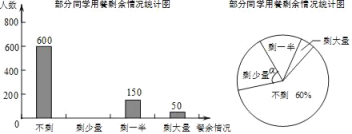
(1)这次被调查的同学共有 人;
(2)补全条形统计图,并在图上标明相应的数据;
(3)扇形统计图中圆心角α= 度;
(4)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐.
查看答案和解析>>
科目:初中数学 来源: 题型:
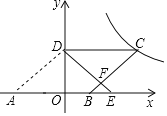
【题目】如图,在平面直角坐标系中,O为坐标原点,ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限.将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F.若y=![]() (k≠0)图象经过点C,且S△BEF=
(k≠0)图象经过点C,且S△BEF=![]() ,则k的值为_____.
,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列四个条件:
①∠EBO=∠DCO;②BE=CD;③OB=OC;④OE=OD.
从上述四个条件中,选取两个条件,不能判定△ABC是等腰三角形的是:( )
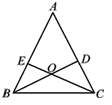
A. ①②B. ①③C. ③④D. ②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com