
【题目】如图①,直线l:y=mx+n(m<0,n>0)与x、y轴分别相交于A、B两点,将△AOB绕点O逆时针旋转90°得到△COD,过点A、B、D的抛物线P叫做l的关联抛物线,而l叫做P的关联直线.
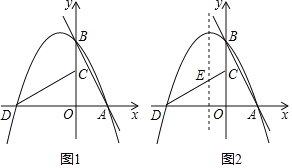
(1)若l:y=﹣2x+2,则P表示的函数解析式为 ;若P:y=﹣x2﹣3x+4,则l表示的函数解析式为 .
(2)求P的对称轴(用含m、n的代数式表示);
(3)如图②,若l:y=﹣2x+4,P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上.当以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标.
【答案】(1)y=﹣x2﹣x+2;y=﹣4x+4;(2)![]() ;(3)满足条件的点Q坐标为
;(3)满足条件的点Q坐标为![]() 、
、![]() .
.
【解析】
(1)若l:y=-2x+2,求出点A、B、D的坐标,利用待定系数法求出P表示的函数解析式;若P:y=-x2-3x+4,求出点D、A、B的坐标,再利用待定系数法求出l表示的函数解析式;
(2)根据对称轴的定义解答即可;
(3)以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,则有FQ∥CE,且FQ=CE.以此为基础,列方程求出点Q的坐标.
解:(1)若l:y=﹣2x+2,则A(1,0),B(0,2).
∵将△AOB绕点O逆时针旋转90°,得到△COD,
∴D(﹣2,0).
设P表示的函数解析式为:y=ax2+bx+c,将点A、B、D坐标代入得:
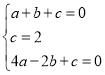 ,
,
解得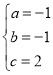 ,
,
∴P表示的函数解析式为:y=﹣x2﹣x+2;
若P:y=﹣x2﹣3x+4=﹣(x+4)(x﹣1),
则D(﹣4,0),A(1,0).
∴B(0,4).
设l表示的函数解析式为:y=kx+b,将点A、B坐标代入得:
![]() ,解得
,解得![]() ,
,
∴l表示的函数解析式为:y=﹣4x+4.
故答案为:y=﹣x2﹣x+2;y=﹣4x+4.
(2)直线l:y=mx+n,(m<0,n>0)与x、y轴分别相交于A、B两点,
∴![]() ,B(0,n),D(﹣n,0).
,B(0,n),D(﹣n,0).
设抛物线对称轴与x轴的交点为N(x,0).
∵DN=AN.
∴![]() ,
,
∴![]() ,
,
∴p的对称轴为![]() .
.
(3)l:y=﹣2x+4,
当x=0时,y=4;当y=0时,x=2,
∴A(2,0)、B(0,4).
∵OC=OA,OD=OB,
∴C(0,2),D(﹣4,0).
设yCD=k1x+b1,
∴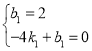 ,
,
∴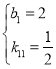
∴直线CD的解析式为:![]() .
.
由(2)可得,p的对称轴为x=﹣1.
∵以点C、E、Q、F为顶点的四边形是以CE为一边的平行四边形.
∴FQ∕∕CE,且FQ=CE.
设直线FQ的解析式为:![]() .
.
∵点E、点C的横坐标相差1.
∴点F、点Q的横坐标也是相差1.
则|xF﹣(﹣1)|=|xF+1|=1.
解得xF=0或xF=﹣2.
∵点F在直线l1:y=﹣2x+4上.
∴点F坐标为(0,4)或(﹣2,8).
若F(0,4),
∴b=4,
∴直线FQ的解析式为:![]() .
.
当x=﹣1时,![]() .
.
∴![]() .
.
若F(﹣2,8),
∴8=-1+b,
∴b=9,
∴直线FQ的解析式为:![]() .
.
当x=﹣1时,![]() ,
,
∴![]() .
.
∴满足条件的点Q坐标为![]() 、
、![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点1000m的C地去,先沿北偏东70°方向到达B地,然后再沿北偏西20°方向走了500m到达目的地C,此时小霞在营地A的( )

A.北偏东20°方向上B.北偏东30°方向上
C.北偏东40°方向上D.北偏西30°方向上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张扑克牌的点数分别是2、3、4、8,将它们洗匀后背面朝上放在桌面上.
(1)从中随机抽取一张牌,求这张牌的点数是偶数的概率;
(2)从中先随机抽取一张牌,接着再抽取一张牌,求这两张牌的点数都是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
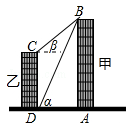
【题目】如图,线段AB、CD分别表示甲乙两建筑物的高,BA⊥AD,CD⊥DA,垂足分别为A、D.从D点测到B点的仰角α为60°,从C点测得B点的仰角β为30°,甲建筑物的高AB=30米
(1)求甲、乙两建筑物之间的距离AD.
(2)求乙建筑物的高CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有4个标有![]() ,2,3,4的小球,它们的形状、大小、质地完全相同,小李从布袋里随机取出一个小球,记下数字为x,小张在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
,2,3,4的小球,它们的形状、大小、质地完全相同,小李从布袋里随机取出一个小球,记下数字为x,小张在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)落在第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
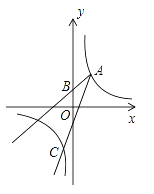
【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y= ![]() 的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
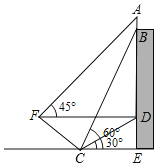
【题目】为积极参与文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图。小明同学为测量宣传牌的高度AB,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A、B、D、E在同一直线上)。然后,小明沿坡度i=1:1.5的斜坡从C走到F处,此时DF正好与地面CE平行。
(1)求点F到直线CE的距离(结果保留根号);
(2)若小明在F处又测得宣传牌顶部A的仰角为45°,求宣传牌的高度AB(结果精确到0.1米,![]() )。
)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com