
【题目】在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点1000m的C地去,先沿北偏东70°方向到达B地,然后再沿北偏西20°方向走了500m到达目的地C,此时小霞在营地A的( )

A.北偏东20°方向上B.北偏东30°方向上
C.北偏东40°方向上D.北偏西30°方向上
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】(知识回顾)我们学习完《直角三角形的边角关系》之后知道,在![]() 中,当锐角
中,当锐角![]() 确定时,锐角
确定时,锐角![]() 的三角函数值也随之确定.结合课本所学知识,请你填空:
的三角函数值也随之确定.结合课本所学知识,请你填空:![]() ______;
______;![]() ______;
______;![]() ______.
______.
(深入探究)定义:在![]() 中,
中,![]() ,我们把
,我们把![]() 的对边与
的对边与![]() 的对边的比叫做
的对边的比叫做![]() 的邻弦,记作
的邻弦,记作![]() ,即:
,即:![]() .请解答下列问题:已知:在
.请解答下列问题:已知:在![]() 中,
中,![]() .
.
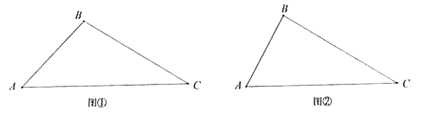
(1)如图①,若![]() ,求
,求![]() 的值;
的值;
(2)如图②,若![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() 是锐角,请你直接写出
是锐角,请你直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
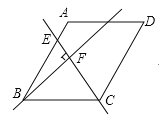
【题目】如图,在菱形ABCD中,![]() ,
,![]() ,点E是AB边上的动点,过点B作直线CE的垂线,垂足为F,当点E从点A运动到点B时,点F的运动路径长为( )
,点E是AB边上的动点,过点B作直线CE的垂线,垂足为F,当点E从点A运动到点B时,点F的运动路径长为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
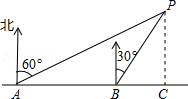
【题目】如图,小明同学在东西方向的环海路A处,测得海中灯塔P在它的北偏东60°方向上,在A的正东200米的B处,测得海中灯塔P在它的北偏东30°方向上.问:灯塔P到环海路的距离PC约等于多少米?(![]() 取1.732,结果精确到1米)
取1.732,结果精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
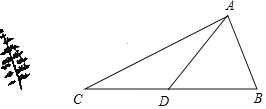
【题目】某校一棵大树发生一定的倾斜,该树与地面的夹角∠ABC=75°.小明测得某时大树的影子顶端在地面C处,此时光线与地面的夹角∠ACB=30°;又过了一段时间,测得大树的影子顶端在地面D处,此时光线与地面的夹角∠ADB=50°.若CD=8米,求该树倾斜前的高度(即AB的长度).(结果保留一位小数.参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线l:y=mx+n(m<0,n>0)与x、y轴分别相交于A、B两点,将△AOB绕点O逆时针旋转90°得到△COD,过点A、B、D的抛物线P叫做l的关联抛物线,而l叫做P的关联直线.
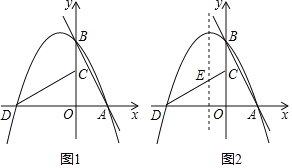
(1)若l:y=﹣2x+2,则P表示的函数解析式为 ;若P:y=﹣x2﹣3x+4,则l表示的函数解析式为 .
(2)求P的对称轴(用含m、n的代数式表示);
(3)如图②,若l:y=﹣2x+4,P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上.当以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com