Question

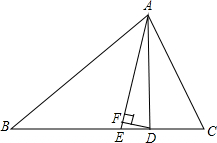
16．△ABC中，∠B=30°，∠C=58°，AE平分∠BAC，AD⊥BC于D，DF⊥AE于F，求∠ADF．

Answer 1

分析 根据三角形内角和定理求出∠BAC，根据角平分线定义求出∠CAE，根据三角形内角和定理求出∠CAD，求出∠DAE，根据三角形内角和定理求出即可．

解答 解：∵在△ABC中，∠B=30°，∠C=58°，
∴∠BAC=180°-∠B-∠C=92°，
∵AE平分∠BAC，
∴∠CAE=$\frac{1}{2}∠$BAC=$\frac{1}{2}×$92°=46°，
∵AD⊥BC，
∴∠ADC=90°，
∴∠DAC=90°-∠C=90°-58°°=32°，
∴∠DAF=∠CAE-∠CAD=46°-32°=14°，
∵DF⊥AE，
∴∠AFD=90°，
∴∠ADF=90°-∠DAE=90°-14°=76°．

点评 本题考查了三角形内角和定理，垂直定义，角平分线性质的应用，能根据三角形的内角和定理求出各个角的度数是解此题的关键，注意：三角形的内角和等于钱180°．