
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
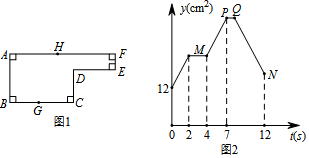
���� �ٸ�������ã�����P��GC���˶���ʱ����2�룬���ɶ�����ٶȣ��ɵ�GC��BC�ij���
�ڢ��ɣ�1���ɵ�BC�ij�������AB=6cm�����Լ������ABP������������жϢڢۣ�
�ܸ�������ã�����P��DE���˶���ʱ����3�룬���ɶ�����ٶȣ��ɵ�DE��������ͼ2�е�Q���ʾ��8��ʱ������ͼ2�е�N���ʾ��12��ʱ����ʾ��P����H�㣬���ɵó���ABP�������
��� �⣺���ݺ���ͼ�����֪����0��2��y��x���������������2�룬P�˶���4cm�����CG=4cm��BC=8cm���ʢ���ȷ��
P��CD��ʱ���ױ�AB���䣬�߲��䣬���������䣬��ͼ���֪CD=2��2=4cm�����y=$\frac{1}{2}$��6��8=24cm2���ʢ���ȷ���۴���
��ͼ2֪����4��t��7ʱ����P��DE���˶���
��DE=2��3=6��
��EF=AB-CD=2��
���Q��Ӧ��ʱ��t=8��
���P�ӵ�F����H�˶��ľ���FH=2����12-8��=8��
��AH=BC+DE-FH=8+6-8=6��
��ͼ2�е�N���ʾ��12��ʱ����ʾ��P����H�㣬��ABP�������$\frac{1}{2}$��6��6=18cm2���ʢ���ȷ��
��ѡ��C��
���� ���⿼���˶�������ĺ���ͼ��Ҫ�ܸ��ݺ���ͼ������ʺ�ͼ���ϵ����ݷ����ó����������ͺ�����Ҫ�����������ʵ������õ���ȷ�Ľ��ۣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
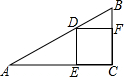 ��ͼ���ڡ�ABC�У���C=90�㣬�ı���EDFCΪ�ڽ������Σ�AC=5��BC=3����AE��DF=5��3��
��ͼ���ڡ�ABC�У���C=90�㣬�ı���EDFCΪ�ڽ������Σ�AC=5��BC=3����AE��DF=5��3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
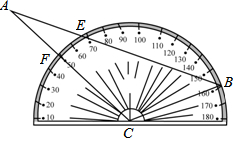 ������������ͼ��ʾ�ķ�ʽ������������ֽƬ�ϣ�ʹ��C�ڰ�ԲԲ���ϣ���B�ڰ�Բ�ϣ���E��F��B�Ķ����ֱ�Ϊ50�㡢70�㡢160�㣬���A�Ķ���ԼΪ��������
������������ͼ��ʾ�ķ�ʽ������������ֽƬ�ϣ�ʹ��C�ڰ�ԲԲ���ϣ���B�ڰ�Բ�ϣ���E��F��B�Ķ����ֱ�Ϊ50�㡢70�㡢160�㣬���A�Ķ���ԼΪ��������| A�� | 10�� | B�� | 20�� | C�� | 25�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com