练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．在-5，0，π，$\sqrt{2}$这四个数中，最大的有理数的是（　　）
    A．-5B．0C．πD．$\sqrt{2}$

    分析 先找出四个数中的有理数，再比较大小即可．

    解答 解：-5，0，π，$\sqrt{2}$这四个数中，有理数是-5，0，
    ∵-5＜0，
    ∴这四个数中最大的有理数的是0．
    故选B．

    点评 本题考查的是实数的大小比较，熟知负数都小于0是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    12．以下列各组数据为边长，可以构成等腰三角形的是（　　）
    A．2，3，4B．5，5，10C．2，2，1D．1，2，3

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．某中学八年级同学在综合实践学习课上，做大蒜在相同条件下的发芽实验，结果统计如表，则试验中大蒜发芽的概率估计是0.95（精确到0.01）．
     种子粒数 100500 1000 2000 3000 
     发芽粒数 96470 948 1912 2853 
     发芽频率 0.960.94 0.948 0.956 0.951 

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，在△ABC中，∠B=45°，∠C=75°，AC=2$\sqrt{6}$，AC的中点为D，若长度为3的线段PQ（P在Q的左侧）在直线BC上滑动，则AP+DQ的最小值为$\frac{3\sqrt{10}+\sqrt{30}}{2}$．．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．（1）计算：|$\sqrt{3}$-2|+$\root{3}{-8}$+$\sqrt{（-2）^{2}}$-|-2|
    （2）解方程（2x-1）2=25．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知关于x的一元二次方程mx2+（3m+1）x+3=0．
    （1）求证：该方程有两个实数根；
    （2）如果抛物线y=mx2+（3m+1）x+3与x轴交于A、B两个整数点（点A在点B左侧），且m为正整数，求此抛物线的表达式；
    （3）在（2）的条件下，抛物线y=mx2+（3m+1）x+3与y轴交于点C，点B关于y轴的对称点为D，设此抛物线在-3≤x≤-$\frac{1}{2}$之间的部分为图象G，如果图象G向右平移n（n＞0）个单位长度后与直线CD有公共点，求n的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．计算：
    （1）6xy$•\frac{{y}^{2}}{15{x}^{2}}$；
    （2）$\frac{-4xy}{9x{y}^{3}}÷\frac{1}{3{x}^{2}}$；
    （3）$\frac{1}{x}÷\frac{1}{x-{x}^{2}}$；
    （4）（a2-ab）$÷\frac{b-a}{ab}$；
    （5）$\frac{{x}^{2}-4{y}^{2}}{{x}^{2}+4x+4}$•$\frac{x+2}{3{x}^{2}+6xy}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

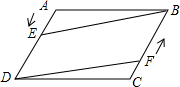    11．如图，在?ABCD中，点E从A向D运动，点F从C向B运动，点E的运动速度m与点F的运动速度n满足m=n关系时，四边形BEDF为平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

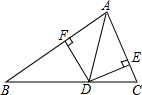    14．如图，点D是BC边上的点，DE⊥AB于E，DF⊥AC于F，AE=AF，连接AD，已知△ABD的面积为s1，△ACD的面积为s2，BC=a，AC=b，AB=c．
    （1）求证：DE=DF；
    （2）求证：$\frac{{s}_{1}}{{s}_{2}}$=$\frac{c}{b}$；
    （2）求BD的长．

    查看答案和解析>>

    同步练习册答案