
 ��֪����x��һԪ���η���mx2+��3m+1��x+3=0��
��֪����x��һԪ���η���mx2+��3m+1��x+3=0������ ��1������������б�ʽ�����жϡ���ȡֵ��Χ�����ɵ�֤��
��2�����������ʽ��ʾ�������������⣬���m��ֵ���ɵ������ߵĽ���ʽ��
��3���������A��B��C��D�����꣬���ݴ���ϵ�������ֱ��CD�Ľ���ʽ����ƽ�ƺ�A��E�Ķ�Ӧ��ֱ�ΪA�䣨-3+n��0����E�䣨-$\frac{1}{2}$+n��$\frac{5}{4}$�������ݵ���ֱ���ϣ����ȡֵ��Χ���ɣ�
��� ��1��֤�����ɸ����б�ʽ���ɵã���=��3m+1��2-4��m��3=��3m-1��2��
�ߣ�3m-1��2��0��
�����0��
��ԭ����������ʵ������
��2���⣺��y=0����ômx2+��3m+1��x+3=0��
��ã�x1=-3��x2=-$\frac{1}{m}$��
����������x����������ĺ������Ϊ��������mΪ��������
��m=1��
�������ߵĽ���ʽΪ��y=x2+4x+3��
��3����ͼ��
�ߵ�x=0ʱ��y=3��
��C��0��3����
�ߵ�y=0ʱ��x1=-3��x2=-1��
�֡ߵ�A�ڵ�B����࣬
��A��-3��0����B��-1��0����
�ߵ�D���B����y��Գƣ�
��D��1��0����
��ֱ��CD�Ľ���ʽΪ��y=kx+b��
��$\left\{\begin{array}{l}{k+b=0}\\{b=3}\end{array}\right.$����ã�$\left\{\begin{array}{l}{k=-3}\\{b=3}\end{array}\right.$��
��ֱ��CD�ı���ʽΪ��y=-3x+3��
�֡ߵ�x=-$\frac{1}{2}$ʱ��y=$��-\frac{1}{2}��^{2}+4����-\frac{1}{2}��+3=\frac{5}{4}$��
���E��-$\frac{1}{2}$��$\frac{5}{4}$����
��ƽ�ƺ�A��E�Ķ�Ӧ��ֱ�ΪA�䣨-3+n��0����E�䣨-$\frac{1}{2}$+n��$\frac{5}{4}$����
��ֱ��y=-3x+3������A�䣨-3+n��0��ʱ���ã�-3��-3+n��+3=0����ã�n=4��
��ֱ��y=-3x+3������E�䣨-$\frac{1}{2}$+n��$\frac{5}{4}$����ʱ���ã�-3��-$\frac{1}{2}$+n��+3=$\frac{5}{4}$����ã�n=$\frac{13}{12}$��
��n��ȡֵ��Χ��$\frac{13}{12}$��n��4��
���� ������Ҫ����һԪ���η��̵Ľⷨ����������x��Ľ��㼰���κ�����ͼ������ʣ���֪��������x��Ľ�������ĺ����꼴��Ӧ��һԪ���η��̵Ľ��ǽ������Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x-2��y-2 | B�� | $\frac{x}{2}$$��\frac{y}{2}$ | C�� | x+2��y+2 | D�� | -2x��-2y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -5 | B�� | 0 | C�� | �� | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
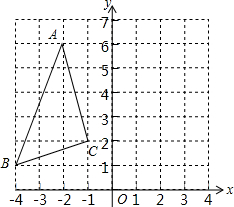 ��ͼ���������ABC������ƽ��1����λ���ȣ�����ԭ��O˳ʱ����ת90�㣬�õ���A1B1C1����ô��A�Ķ�Ӧ��A1������Ϊ��������
��ͼ���������ABC������ƽ��1����λ���ȣ�����ԭ��O˳ʱ����ת90�㣬�õ���A1B1C1����ô��A�Ķ�Ӧ��A1������Ϊ��������| A�� | ��1��3�� | B�� | ��2��0�� | C�� | ��6��1�� | D�� | ��6��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com