
分析 举反例可知“如果两个角是同位角,那么这两个角相等”这个命题是假命题;根据以“如果…,那么…”的形式叙述的命题,“如果”后面接的部分是题设,“那么”后面解的部分是结论即可求解.
解答 解:如图,∠1与∠2是同位角,但是∠1≠∠2,所以如果两个角是同位角,那么这两个角相等,是假命题,
此命题的题设是两个角是同位角,结论是这两个角相等.
故答案为假,两个角是同位角,这两个角相等.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”的形式,这时,“如果”后面接的部分是题设,“那么”后面解的部分是结论.也考查了命题的真假判断.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:选择题
| A. | 999 | B. | 999.5 | C. | 1000 | D. | 1000.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 种子粒数 | 100 | 500 | 1000 | 2000 | 3000 |
| 发芽粒数 | 96 | 470 | 948 | 1912 | 2853 |
| 发芽频率 | 0.96 | 0.94 | 0.948 | 0.956 | 0.951 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
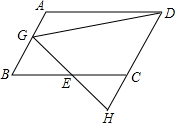 如图,在?ABCD中,E为BC中点,过点E作EG⊥AB于G,连结DG,延长DC,交GE的延长线于点H.已知BC=10,∠GDH=45°,DG=8$\sqrt{2}$.求CD的长.
如图,在?ABCD中,E为BC中点,过点E作EG⊥AB于G,连结DG,延长DC,交GE的延长线于点H.已知BC=10,∠GDH=45°,DG=8$\sqrt{2}$.求CD的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠B=45°,∠C=75°,AC=2$\sqrt{6}$,AC的中点为D,若长度为3的线段PQ(P在Q的左侧)在直线BC上滑动,则AP+DQ的最小值为$\frac{3\sqrt{10}+\sqrt{30}}{2}$..
如图,在△ABC中,∠B=45°,∠C=75°,AC=2$\sqrt{6}$,AC的中点为D,若长度为3的线段PQ(P在Q的左侧)在直线BC上滑动,则AP+DQ的最小值为$\frac{3\sqrt{10}+\sqrt{30}}{2}$..查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知关于x的一元二次方程mx2+(3m+1)x+3=0.
已知关于x的一元二次方程mx2+(3m+1)x+3=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com