
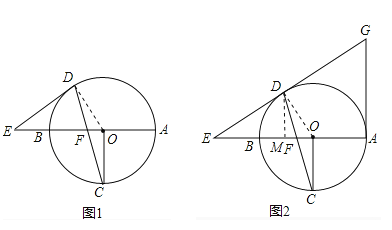
【题目】(8分)已知AB为⊙O的直径,OC⊥AB,弦DC与OB交于点F,在直线AB上有一点E,连接ED,且有ED=EF.

(1)如图①,求证:ED为⊙O的切线;
(2)如图②,直线ED与切线AG相交于G,且OF=2,⊙O的半径为6,求AG的长.
【答案】(1)见解析;(2)12
【解析】试题分析:(1)连接OD,由ED=EF可得出∠EDF=∠EFD,由对顶角相等可得出∠EDF=∠CFO;由OD=OC可得出∠ODF=∠OCF,结合OC⊥AB即可得知∠EDF+∠ODF=90°,即∠EDO=90°,由此证出ED为⊙O的切线;
(2)连接OD,过点D作DM⊥BA于点M,结合(1)的结论根据勾股定理可求出ED、EO的长度,结合∠DOE的正弦、余弦值可得出DM、MO的长度,根据切线的性质可知GA⊥EA,从而得出DM∥GA,根据相似三角形的判定定理即可得出△EDM∽△EGA,根据相似三角形的性质即可得出GA的长度
试题解析:解:(1)连接OD,∵ED=EF,∴∠EDF=∠EFD,∵∠EFD=∠CFO,∴∠EDF=∠CFO.∵OD=OC,∴∠ODF=∠OCF.∵OC⊥AB,∴∠CFO+∠OCF=∠EDF+∠ODF=∠EDO=90°,∴ED为⊙O的切线;
(2)连接OD,过点D作DM⊥BA于点M,由(1)可知△EDO为直角三角形,设ED=EF=a,EO=EF+FO=a+2,由勾股定理得,EO2=ED2+DO2,即(a+2)2=a2+62,解得,a=8,即ED=8,EO=10.∵sin∠EOD=![]() ,cos∠EOD=
,cos∠EOD=![]() ,∴DM=ODsin∠EOD=6×
,∴DM=ODsin∠EOD=6×![]() =
=![]() ,MO=ODcos∠EOD=6×
,MO=ODcos∠EOD=6×![]() =
=![]() ,∴EM=EO﹣MO=10﹣
,∴EM=EO﹣MO=10﹣![]() =
=![]() ,EA=EO+OA=10+6=16.
,EA=EO+OA=10+6=16.
∵GA切⊙O于点A,∴GA⊥EA,∴DM∥GA,∴△EDM∽△EGA,∴ ![]() ,即
,即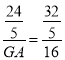 ,解得GA=12.
,解得GA=12.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读下列短文:
如图,G是四边形ABCD对角线AC上一点,过G作GE∥CD交AD于E,GF∥CB交AB于F,若EG=FG,则有BC=CD成立,同时可知四边形ABCD与四边形AFGE相似.

解答问题:
(1)有一块三角形空地(如图△ABC),BC邻近公路,现需在此空地上修建一个正方形广场,其余地为草坪,要使广场一边靠公路,且其面积最大,如何设计,请你在下面图中画出此广场正方形.(尺规作图,不写作法)
(2)锐角△ABC是一块三角形余料,边AB=130mm,BC=150mm,AC=140mm,要把它加工成正方形零件,使正方形的一边在三角形的一边上,其余两个顶点分别在另外两条边上,且剪去正方形零件后剩下的边角料较少,这个正方形零件的边长是多少?你能得出什么结论,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗洪指挥部的一位驾驶员接到一个防洪的紧急任务,要在限定的时内把一批抗洪物质从物质局运到水库,这辆车如果按每小时30千米的速度行驶在限定的时间内赶到水库,还差3千米,他决定以每小时40千米的速度前进,结果比限定时间早到18分钟,问限定时间是几小时?物质局仓库离水库有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数是( )

A. 400 B. 450 C. 500 D. 600
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx-2的图象与x轴交于A,B两点,与y轴交于点C,点A的坐标为(4,0),且当x=-2和x=5时二次函数的函数值y相等.

(1)求实数a,b的值;
(2)如图①,动点E,F同时从A点出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒![]() 个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.
个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.
①是否存在某一时刻t,使得△DCF为直角三角形?若存在,求出t的值;若不存在,请说明理由;
②设△DEF与△ABC重叠部分的面积为S,求S关于t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小莉的爸爸买了某演唱会的一张门票,她和哥哥两人都想去观看,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,将数字 1,2,3,5 的四张牌给小莉,将数字为 4,6,7,8 的四张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后 将抽出的两张牌数字相加,如果和为偶数,则小莉去,如果和为奇数,则哥哥去。
(1)请用树状图或列表的方法表示出两张牌数字相加和的所有可能出现的结果;
(2)哥哥设计的游戏规则公平么?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系xOy中,函数y1=![]() (x>0)的图象与一次函数y2=kx-k的图象的交点为A(m,2).
(x>0)的图象与一次函数y2=kx-k的图象的交点为A(m,2).
(1)求一次函数的解析式;
(2)设一次函数y=kx-k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是6,请写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某实验学校校友会在今年开学初,到新华书店采购文学名著和自然科学两类图书.经了解,购买30本文学名著和50本自然科学书共需2350元,20本文学名著比20本自然科学书贵500元.
(1)求每本文学名著和自然科学书的单价.
(2)若该校校友会要求购买自然科学书比文学名著多30本,总费用不超过2400元,请求出至多购买文学名著多少本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com