
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为cm. 
【答案】42
【解析】解:∵将△ABC绕点B顺时针旋转60°,得到△BDE, ∴△ABC≌△BDE,∠CBD=60°,
∴BD=BC=12cm,
∴△BCD为等边三角形,
∴CD=BC=CD=12cm,
在Rt△ACB中,AB= ![]() =13,
=13,
△ACF与△BDF的周长之和=AC+AF+CF+BF+DF+BD=AC+AB+CD+BD=5+13+12+12=42(cm),
故答案为:42.
根据将△ABC绕点B顺时针旋转60°,得到△BDE,可得△ABC≌△BDE,∠CBD=60°,BD=BC=12cm,从而得到△BCD为等边三角形,得到CD=BC=CD=12cm,在Rt△ACB中,利用勾股定理得到AB=13,所以△ACF与△BDF的周长之和=AC+AF+CF+BF+DF+BD=AC+AB+CD+BD,即可解答.


科目:初中数学 来源: 题型:
【题目】如图所示,在△ACB中,∠ACB=90゜,CD⊥AB于D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F , 求证:∠CEF=∠CFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,AB=1,在BC上取一点E , 沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=( ).
A.![]()
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点(2,0)和(﹣3.5,0),顶点为(﹣1,4),根据图象直接写出下列答案. 
(1)方程ax2+bx+c=0的两个根;
(2)不等式ax2+bx+c<0的解集;
(3)若方程ax2+bx+c=k有两个不相等实根,则k的取值范围是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为( ) 
A.60°
B.75°
C.85°
D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使点A′恰好落在AB上,则旋转角度为( ) 
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).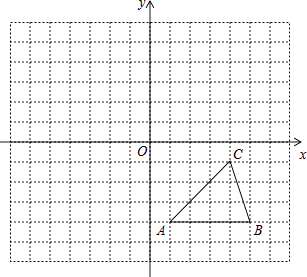
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1 , 画出△A1B1C1 , 并写出C1的坐标.
(2)以点B为位似中心在格纸内画出△A2BC2 , 且与△ABC的位似比为2:1,并写出C2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com