
【题目】如图所示,在△ACB中,∠ACB=90゜,CD⊥AB于D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F , 求证:∠CEF=∠CFE.
【答案】
(1)
证明:∵∠ACB=90゜,CD⊥AB于D,
∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,
∴∠ACD=∠B;
(2)
在Rt△AFC中,∠CFA=90°-∠CAF,
同理在Rt△AED中,∠AED=90°-∠DAE.
又∵AF平分∠CAB,
∴∠CAF=∠DAE,
∴∠AED=∠CFE,
又∵∠CEF=∠AED,
∴∠CEF=∠CFE.
【解析】(1)由于∠ACD与∠B都是∠BCD的余角,根据同角的余角相等即可得(2)根据直角三角形两锐角互余得出∠CFA=90°-∠CAF , ∠AED=90°-∠DAE , 再根据角平分线的定义得出∠CAF=∠DAE , 然后由对顶角相等的性质,等量代换即可证明∠CEF=∠CFE.
【考点精析】掌握解直角三角形是解答本题的根本,需要知道解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3 ![]() 米,坡顶有旗杆BC , 旗杆顶端B点与A点有一条彩带相连 . 若AB=10米,则旗杆BC的高度为( )
米,坡顶有旗杆BC , 旗杆顶端B点与A点有一条彩带相连 . 若AB=10米,则旗杆BC的高度为( )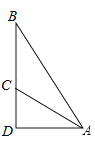
A.5米
B.6米
C.8米
D.(3+ ![]() )米
)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB , 坡面AC的倾斜角为45° . 为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i= ![]() :3 . 若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3 . 若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)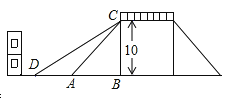
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请回答下列问题:
(1)叙述三角形中位线定理,并运用平行四边形的知识证明;
(2)运用三角形中位线的知识解决如下问题:如图,在四边形ABCD中,AD∥BC , E、F分别是AB , CD的中点,求证:EF= ![]() (AD+BC)
(AD+BC)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为cm. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com