
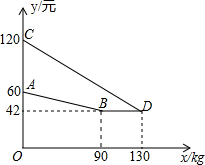
 某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD表示该产品每千克生产成本y1(单位:元)与产量x(单位:kg)之间的函数关系;线段CD表示每千克的销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD表示该产品每千克生产成本y1(单位:元)与产量x(单位:kg)之间的函数关系;线段CD表示每千克的销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.分析 (1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;
(2)根据线段AB经过的两点的坐标利用待定系数法确定一次函数的表达式即可;
(3)利用总利润=单位利润×产量列出有关x的二次函数,求得最值即可.
解答 解:(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;
(2)设线段AB所表示的y1与x之间的函数关系式为y=k1x+b1,
∵y=k1x+b1的图象过点(0,60)与(90,42),
∴$\left\{\begin{array}{l}{{b}_{1}=60}\\{90{k}_{1}+{b}_{1}=42}\end{array}\right.$,
∴解得:$\left\{\begin{array}{l}{{k}_{1}=-0.2}\\{{b}_{1}=60}\end{array}\right.$,
∴这个一次函数的表达式为;y=-0.2x+60(0≤x≤90);
(3)设y2与x之间的函数关系式为y=k2x+b2,
∵经过点(0,120)与(130,42),
∴$\left\{\begin{array}{l}{{b}_{2}=120}\\{130{k}_{2}+{b}_{2}=42}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=-0.6}\\{{b}_{2}=120}\end{array}\right.$,
∴这个一次函数的表达式为y2=-0.6x+120(0≤x≤130),
设产量为xkg时,获得的利润为W元,
当0≤x≤90时,W=x[(-0.6x+120)-(-0.2x+60)]=-0.4(x-75)2+2250,
∴当x=75时,W的值最大,最大值为2250;
当90≤x≤130时,W=x[(-0.6x+120)-42]=-0.6(x-65)2+2535,
由-0.6<0知,当x>65时,W随x的增大而减小,∴90≤x≤130时,W≤2160,
∴当x=90时,W=-0.6(90-65)2+2535=2160,
因此当该产品产量为75kg时,获得的利润最大,最大值为2250.
故答案为:w=-0.4(x-75)2+2250;w=-0.6(x-65)2+2535,75,2250.
点评 本题考查了二次函数的应用,解题的关键是从实际问题中抽象出二次函数模型,难度不大.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
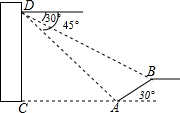 如图,楼房与斜坡AB之间有一条小河,在搂房上的点D处测得斜坡的坡脚A点的俯角为45°,测得斜坡的顶端B点的俯角为30°,若观测点D距地面的高度CD=30米,斜坡的坡角为30°,试求斜坡AB的长(结果保留根号).
如图,楼房与斜坡AB之间有一条小河,在搂房上的点D处测得斜坡的坡脚A点的俯角为45°,测得斜坡的顶端B点的俯角为30°,若观测点D距地面的高度CD=30米,斜坡的坡角为30°,试求斜坡AB的长(结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com