
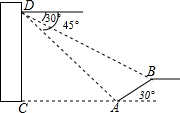
 如图,楼房与斜坡AB之间有一条小河,在搂房上的点D处测得斜坡的坡脚A点的俯角为45°,测得斜坡的顶端B点的俯角为30°,若观测点D距地面的高度CD=30米,斜坡的坡角为30°,试求斜坡AB的长(结果保留根号).
如图,楼房与斜坡AB之间有一条小河,在搂房上的点D处测得斜坡的坡脚A点的俯角为45°,测得斜坡的顶端B点的俯角为30°,若观测点D距地面的高度CD=30米,斜坡的坡角为30°,试求斜坡AB的长(结果保留根号). 分析 过点B作BE⊥CD于点E、作BF⊥CA于点F,设BF=x米,在RT△ABF中表示出AB、AF的长,在RT△ACD中求出AC的长,进而可得BE、DE的长,在RT△BDE中由tan∠DBE=$\frac{DE}{BE}$列出关于x的方程,解方程可得x的值即可.
解答 解:过点B作BE⊥CD于点E,作BF⊥CA于点F,
则四边形CEBF是矩形,
设BF=x米,
∵∠BAF=30°,
∴AB=2BF=2x米,AF=$\sqrt{A{B}^{2}-B{F}^{2}}$=$\sqrt{3}x$米,
又∵CD=30米,∠CAD=45°,
∴AC=CD=30米,
∵四边形CEBF是矩形,
∴BE=CF=CA+AF=30+$\sqrt{3}$x(米),BF=CE=x,DE=30-x(米),
在RT△BDE中,∵∠DBE=30°,
∴tan∠DBE=$\frac{DE}{BE}$,即$\frac{30-x}{30+\sqrt{3}x}$=$\frac{\sqrt{3}}{3}$,
解得:x=15-5$\sqrt{3}$,
则AB=2x=30-10$\sqrt{3}$(米),
答:斜坡AB的长为(30-10$\sqrt{3}$)米.
点评 本题考查了仰角、坡角的定义,解直角三角形的应用,能借助仰角构造直角三角形,并结合图形利用三角函数解直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
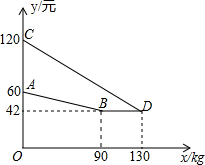 某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD表示该产品每千克生产成本y1(单位:元)与产量x(单位:kg)之间的函数关系;线段CD表示每千克的销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD表示该产品每千克生产成本y1(单位:元)与产量x(单位:kg)之间的函数关系;线段CD表示每千克的销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在数轴上点A表示1,现将点A沿x轴做如下移动:第一次点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种移动规律移动下去,則线段A13A14的长度是42.
如图,在数轴上点A表示1,现将点A沿x轴做如下移动:第一次点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种移动规律移动下去,則线段A13A14的长度是42.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com