
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①将x=-2代入y=ax2+bx+c,可以结合图象得出x=-2时,y<0;
②由y=ax2+bx+c(a≠0)的图象经过点(-1,2),a-b+c=2,与y轴交于(0,2)点,c=2,从而得出a-b=0,二次函数的开口向下,a<0,∴2a-b<0;
③根据函数与x轴交点的横坐标分别为x1、x2,其中-2<x1<-1,0<x2<1,可以得出两根的近似值,从而代入函数解析式,得出a,b,的值;得出a<-1;
④利用③的解析式得出,b2+8a>4ac.
解答 解:二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),与y轴交于(0,2)点,且与x轴交点的横坐标分别为x1、x2,其中-2<x1<-1,0<x2<1,下列结论
①4a-2b+c<0;当x=-2时,y=ax2+bx+c,y=4a-2b+c,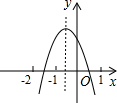
∵-2<x1<-1,∴y<0,故①正确;
②2a-b<0;
∵二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),
∴a-b+c=2,与y轴交于(0,2)点,c=2,
∴a-b=0,二次函数的开口向下,a<0,
∴2a-b<0,故②正确;
③已知抛物线经过(-1,2),即a-b+c=2(1),由图知:当x=1时,y<0,即a+b+c<0(2),
由①知:4a-2b+c<0(3);联立(1)(2),得:a+c<1;联立(1)(3)得:2a-c<-4;
故3a<-3,即a<-1;所以③正确
④由于抛物线的对称轴大于-1,所以抛物线的顶点纵坐标应该大于2,即:$\frac{4ac-{b}^{2}}{4a}$>2,由于a<0,所以4ac-b2<8a,即b2+8a>4ac,故④正确,
故选:D.
点评 此题主要考查了抛物线与x轴的交点坐标性质,以及利用函数图象得出函数与坐标轴的近似值,进而得出函数解析式,这种题型是中考中新题型.


科目:初中数学 来源: 题型:解答题
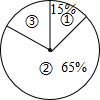 为践行社会主义核心价值观,某市教育局准备举办教室“敬业杯”课堂教学技能大赛,参赛选手均由辖区内各个学校选派,某校首先在校内组织部分教师进行了预赛,并将预赛成绩绘制成了如下不完整的统计图表,请根据图表回答下列问题:
为践行社会主义核心价值观,某市教育局准备举办教室“敬业杯”课堂教学技能大赛,参赛选手均由辖区内各个学校选派,某校首先在校内组织部分教师进行了预赛,并将预赛成绩绘制成了如下不完整的统计图表,请根据图表回答下列问题:| 等级 | 成绩m(分) | 频数 |
| ①优秀 | 95≤m≤100 | 3 |
| ②良好 | 90≤m≤95 | a |
| ③合格 | 85≤m≤90 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
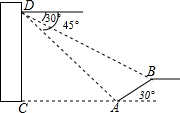 如图,楼房与斜坡AB之间有一条小河,在搂房上的点D处测得斜坡的坡脚A点的俯角为45°,测得斜坡的顶端B点的俯角为30°,若观测点D距地面的高度CD=30米,斜坡的坡角为30°,试求斜坡AB的长(结果保留根号).
如图,楼房与斜坡AB之间有一条小河,在搂房上的点D处测得斜坡的坡脚A点的俯角为45°,测得斜坡的顶端B点的俯角为30°,若观测点D距地面的高度CD=30米,斜坡的坡角为30°,试求斜坡AB的长(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
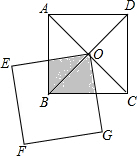 如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点旋转,若两个正方形的边长相等,则两个正方形的重合部分的面积( )
如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点旋转,若两个正方形的边长相等,则两个正方形的重合部分的面积( )| A. | 由小变大 | B. | 由大变小 | ||
| C. | 始终不变 | D. | 先由大变小,然后又由小变大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com