
【题目】
如图,在![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的动点(不与端点重合),点
上的动点(不与端点重合),点![]() 是线段
是线段![]() 上的动点,连接
上的动点,连接![]() 、
、![]() ,若在点
,若在点![]() 、点
、点![]() 的运动过程中,始终保证
的运动过程中,始终保证![]() 。
。
(1)求证:![]() ;
;
(2)当以点![]() 为圆心,以
为圆心,以![]() 为半径的圆与
为半径的圆与![]() 相切时,求
相切时,求![]() 的长;
的长;
(3)探究:在点![]() 、点
、点![]() 的运动过程中,
的运动过程中,![]() 可能为等腰三角形吗?若能,求出
可能为等腰三角形吗?若能,求出![]() 的长;若不能,请说明理由。
的长;若不能,请说明理由。
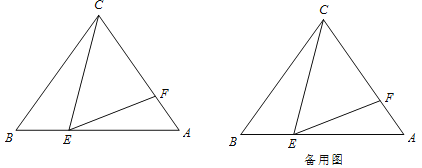
【答案】(1)证明见解析;(2)BE的长为1或5;(3)当BE的长为1或![]() 时,△CFE为等腰三角形.
时,△CFE为等腰三角形.
【解析】试题分析(1)由∠B +∠B CE=∠CEA=∠CEF+∠FEA,∠CEF=∠B即可得∠AEF=∠BCE;(2)设⊙C与BA切于点M,则CM=CF,CM⊥BA(如图),根据等腰三角形的性质可得BM=AM==3,在Rt△AMC中,根据勾股定理可得CF =CM=4,即可得AF=1,再证得△AEF∽△BCE,设设BE长为x,则EA长为6-x,根据相似三角形的性质列出方程求解即可;(3)分CE=CF,CF=EF,CF=EF三种情况求解即可.
试题解析:
(1)证明:∵∠B +∠B CE=∠CEA =∠CEF+∠FEA
∠CEF=∠B
∴∠AEF=∠BCE
(2)设⊙C与BA切于点M,则CM=CF,CM⊥BA
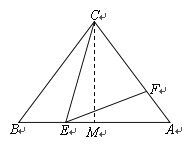
∵CA=CB,CM⊥BA ∴BM=AM=![]() =3
=3
Rt△AMC中,AC=5,AM=3,
∴CF =CM=4 ∴AF=1
∵ CA=CB ∴∠B=∠C
由(1)知∠AEF=∠BCE
∴△AEF∽△BCE
∴![]()
设BE长为x,则EA长为6-x
∴![]()
解得:x1=1,x2=5
答:BE的长为1或5.
(3)可能.

①当CE=CF时,∠3=∠2=∠A
∴EF∥AB,此时E与B重合,与条件矛盾,不成立.
②当CF=EF时,
又∵△AEF∽△BCE
∴△AEF≌△BCE
∴AE=BC=5
∴BE=AB-5=1
③当CF=EF时,∠1=∠2=∠A=∠B
△FCE∽△CBA
∴![]()

∴![]()
∵△AEF∽△BCE
∴![]()
∴![]()
∴![]()
答:当BE的长为1或![]() 时,△CFE为等腰三角形.
时,△CFE为等腰三角形.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】下列调查中,需要全面调查的是( )
A. 对乘坐飞机旅客行李的检查 B. 为了解北京市的空气质量
C. 调查某一批次盒装牛奶的合格情况 D. 了解一批炮弹的杀伤半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
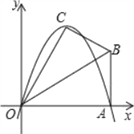
【题目】已知在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
如图,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 。
。
(1)求这两个函数的表达式;
(2)如图1,若![]() ,且其两边分别与两坐标轴的正半轴交于点
,且其两边分别与两坐标轴的正半轴交于点![]() 、点
、点![]() 。求四边形
。求四边形![]() 的面积;
的面积;
(3)如图2,点![]() 是反比例函数
是反比例函数![]() 图象上的一点,过点
图象上的一点,过点![]() 作x轴、
作x轴、![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() ,过
,过![]() 作x轴的垂线,垂足为
作x轴的垂线,垂足为![]() 。设
。设![]() 点的横坐标为
点的横坐标为![]() ,当
,当![]() 时,是否存在点
时,是否存在点![]() ,使得四边形
,使得四边形![]() 为正方形?若存在,求出
为正方形?若存在,求出![]() 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com