
【题目】
如图,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 。
。
(1)求这两个函数的表达式;
(2)如图1,若![]() ,且其两边分别与两坐标轴的正半轴交于点
,且其两边分别与两坐标轴的正半轴交于点![]() 、点
、点![]() 。求四边形
。求四边形![]() 的面积;
的面积;
(3)如图2,点![]() 是反比例函数
是反比例函数![]() 图象上的一点,过点
图象上的一点,过点![]() 作x轴、
作x轴、![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() ,过
,过![]() 作x轴的垂线,垂足为
作x轴的垂线,垂足为![]() 。设
。设![]() 点的横坐标为
点的横坐标为![]() ,当
,当![]() 时,是否存在点
时,是否存在点![]() ,使得四边形
,使得四边形![]() 为正方形?若存在,求出
为正方形?若存在,求出![]() 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。

【答案】(1)这两个函数的表达式分别为:y=x,![]() ;(2)四边形
;(2)四边形![]() 的面积为6;(3)P点坐标为(
的面积为6;(3)P点坐标为(![]() ,
,![]() )
)
【解析】试题分析:(1)将点M(![]() ,
,![]() )分别带入
)分别带入![]() 与
与![]() 求得a、k的值,即可得这两个函数的表达式;(2)过点M分别做x轴、y轴的垂线,垂足分别为C、D,易证△AMC≌△BMD,S四边形OCMD=S四边形OAMB即可求解;(3)设P点坐标为(
求得a、k的值,即可得这两个函数的表达式;(2)过点M分别做x轴、y轴的垂线,垂足分别为C、D,易证△AMC≌△BMD,S四边形OCMD=S四边形OAMB即可求解;(3)设P点坐标为(![]() ),则PE=HG=GE=
),则PE=HG=GE=![]() ,OE=2x,再由∠MOE=45°,可得OG=GH=
,OE=2x,再由∠MOE=45°,可得OG=GH=![]() , 即可得OE= OG+GH=
, 即可得OE= OG+GH=![]() ,根据正方形的性质可得2x=
,根据正方形的性质可得2x=![]() ,解得x的值,即可求得点P的坐标.
,解得x的值,即可求得点P的坐标.
试题解析:
(1)将点M(![]() ,
,![]() )分别带入
)分别带入![]() 与
与![]() 得:
得:
![]() =a
=a![]() ,
,![]()
解得:a=1,k=6
∴这两个函数的表达式分别为:y=x,![]()
(2)过点M分别做x轴、y轴的垂线,垂足分别为C、D.
则∠MCA=∠MDB=90°,∠AMC=∠BMD=90°-∠AMD,MC=MD=![]() ,
,
∴△AMC≌△BMD,
∴S四边形OCMD=S四边形OMB=6;
(3)设P点坐标为(![]() ),则PE=HG=GE=
),则PE=HG=GE=![]() ,OE=2x,
,OE=2x,
∵∠MOE=45°,∴OG=GH=![]() , ∴OE= OG+GH=
, ∴OE= OG+GH=![]()
∴2x=![]()
![]()
∴P点坐标为(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】小强用8块棱长为3 cm的小正方体,搭建了一个如图所示的积木,下列说法中不正确的是( )
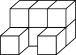
A. 从左面看这个积木时,看到的图形面积是27cm2
B. 从正面看这个积木时,看到的图形面积是54cm2
C. 从上面看这个积木时,看到的图形面积是45cm2
D. 分别从正面、左面、上面看这个积木时,看到的图形面积都是72cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
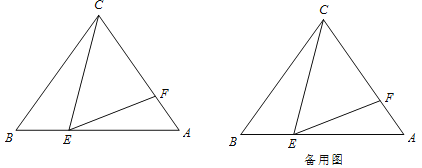
【题目】
如图,在![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的动点(不与端点重合),点
上的动点(不与端点重合),点![]() 是线段
是线段![]() 上的动点,连接
上的动点,连接![]() 、
、![]() ,若在点
,若在点![]() 、点
、点![]() 的运动过程中,始终保证
的运动过程中,始终保证![]() 。
。
(1)求证:![]() ;
;
(2)当以点![]() 为圆心,以
为圆心,以![]() 为半径的圆与
为半径的圆与![]() 相切时,求
相切时,求![]() 的长;
的长;
(3)探究:在点![]() 、点
、点![]() 的运动过程中,
的运动过程中,![]() 可能为等腰三角形吗?若能,求出
可能为等腰三角形吗?若能,求出![]() 的长;若不能,请说明理由。
的长;若不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,先填空后证明. 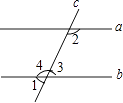
已知:∠1+∠2=180°,求证:a∥b.
证明:∵∠1=∠3 ,
∠1+∠2=180°
∴∠3+∠2=180
∴a∥b
请你再写出另一种证明方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据农业农村部新闻部办公室2018年10月15日消息,江宁省发现疑似非洲猪瘟疫情,此次猪瘟疫情发病急,蔓延速度快.当政府和企业迅速进行了猪瘟疫情排査和处置.在疫情排査过程中.某农场第一天发现3头生猪发病.两天后发现共有363头生猪发病,求每头发病生猪平均每天传染多少头生猪?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉兴教育学院大学生小王利用暑假开展了30天的社会实践活动,参与了嘉兴浙北超市的经营,了解到某成本为15元/件的商品在x天销售的相关信息,如表表示:
销售量p(件) | P=45﹣x |
销售单价q(元/件) | 当1≤x≤18时,q=20+x 当18<x≤30时,q=38 |
设该超市在第x天销售这种商品获得的利润为y元.
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC. 
(1)求证:△BAD≌△ACE;
(2)若∠B=30°,AB=26,BD=10,求平行四边形ABDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com