Question

【题目】嘉兴教育学院大学生小王利用暑假开展了30天的社会实践活动，参与了嘉兴浙北超市的经营，了解到某成本为15元/件的商品在x天销售的相关信息，如表表示：

销售量p（件）	P=45﹣x
销售单价q（元/件）	当1≤x≤18时，q=20+x 当18＜x≤30时，q=38

设该超市在第x天销售这种商品获得的利润为y元．

（1）求y关于x的函数关系式；

（2）在这30天中，该超市销售这种商品第几天的利润最大？最大利润是多少？

Answer 1

【答案】（1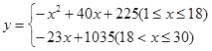）（2）在这30天中，该超市销售这种商品，第18天的利润最大，且最大利润为621元．

【解析】试题分析：（1）根据总价=单价×数量，分别用每件商品的利润乘以这种商品的销售量，求出y关于x的函数关系式即可．

（2）首先分类讨论，求出①当1≤x≤18时，②当18＜x≤30时，该超市销售这种商品所获的利润是多少，然后比较大小，判断出该超市销售这种商品第几天的利润最大，最大利润是多少即可；

试题解析：

（1）①当1≤x≤18时，

y=（20+x﹣15）（45﹣x）

=（5+x）（45﹣x）

=﹣x2+40x+225

②当18＜x≤30时，

y=（38﹣15）（45﹣x）

=23（45﹣x）

=﹣23x+1035

∴

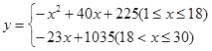
（2）①当1≤x≤18时，y=﹣（x﹣20）2+625，

∴当x=18时，y最大值=621元．

②当18＜x≤30时，

∵﹣30＜0，

∴y随x的增大而减小，

又∵x取正整数，

∴当x=19时，y最大值=598（元）．

∵621＞598，

∴在这30天中，该超市销售这种商品，第18天的利润最大，且最大利润为621元．