【题目】据农业农村部新闻部办公室2018年10月15日消息，江宁省发现疑似非洲猪瘟疫情，此次猪瘟疫情发病急，蔓延速度快．当政府和企业迅速进行了猪瘟疫情排査和处置．在疫情排査过程中.某农场第一天发现3头生猪发病.两天后发现共有363头生猪发病，求每头发病生猪平均每天传染多少头生猪？
考前必练系列答案科目：初中数学 来源： 题型：
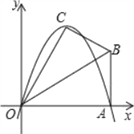
【题目】已知在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴，建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处．
（1）求点C的坐标；
（2）若抛物线y=ax2+bx（a≠0）经过C、A两点，求此抛物线的解析式；
（3）若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M．问:是否存在这样的点P,使得四边形CDPM为等腰梯形？若存在,请求出此时点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
如图，正比例函数
与反比例函数
的图象交于点
。
（1）求这两个函数的表达式；
（2）如图1，若
，且其两边分别与两坐标轴的正半轴交于点
、点
。求四边形
的面积；
（3）如图2，点
是反比例函数图象上的一点，过点作x轴、
轴的垂线，垂足分别为
、
，
交直线
于点
，过作x轴的垂线，垂足为
。设点的横坐标为
，当
时，是否存在点，使得四边形
为正方形？若存在，求出点坐标；若不存在，请说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图，在
中，AC=BC，点D是边AB的中点，E，F分别是AC和BC的中点，分别以CE，CF为一边向上作两个全等的矩形CEGH和矩形CFMN（其中EG=FM），依次连结DG、DM、GM。
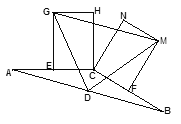
（1）求证：
是等腰三角形。
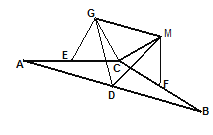
（2）如图，若将上图中的两个全等的矩形改为两个全等的正三角形（
和
)，其他条件不变。请探究的形状，并说明理由。
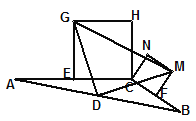
（3）若将上图中的两个全等的矩形改为两个正方形，并把
中的边BC缩短到如图形状，请探究的形状，并说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE、BE分别交于点G、H，∠CBE=∠BAD．有下列结论：①FD=FE；②AH=2CD；③BCAD=
AE2；④∠DFE=2∠DAC ;⑤若连接CH，则CH∥EF.其中正确的个数为（ ）
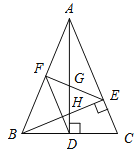
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是定圆O的内接三角形，AD为△ABC的高线，AE平分∠BAC交⊙O于E，交BC于G，连OE交BC于F，连OA，在下列结论中， ①CE＝2EF，②△ABG∽△AEC，③∠BAO＝∠DAC，④
为常量．其中正确的有______．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
