
����Ŀ����֪����ͼ����![]() �У�AC=BC����D�DZ�AB���е㣬E��F�ֱ���AC��BC���е㣬�ֱ���CE��CFΪһ������������ȫ�ȵľ���CEGH�;���CFMN������EG=FM������������DG��DM��GM��
�У�AC=BC����D�DZ�AB���е㣬E��F�ֱ���AC��BC���е㣬�ֱ���CE��CFΪһ������������ȫ�ȵľ���CEGH�;���CFMN������EG=FM������������DG��DM��GM��
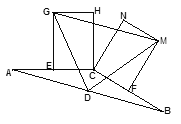
��1����֤��![]() �ǵ��������Ρ�
�ǵ��������Ρ�
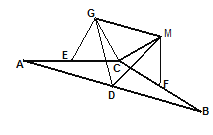
��2����ͼ��������ͼ�е�����ȫ�ȵľ��θ�Ϊ����ȫ�ȵ��������Σ�![]() ��
��![]() )�������������䡣��̽��
)�������������䡣��̽��![]() ����״����˵�����ɡ�
����״����˵�����ɡ�
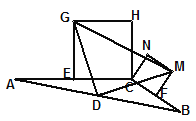
��3��������ͼ�е�����ȫ�ȵľ��θ�Ϊ���������Σ�����![]() �еı�BC���̵���ͼ��״����̽��
�еı�BC���̵���ͼ��״����̽��![]() ����״����˵�����ɡ�
����״����˵�����ɡ�
���𰸡���1��֤�������� ��2����DGM�ǵȱ������Σ� ��3����DGM�ǵ���ֱ�������Σ�
�������������������1���ȸ���SAS֤����FBM�ա�MDH���õ�DG��DM����![]() �ǵ��������Σ���2��������֤
�ǵ��������Σ���2��������֤![]() �ǵ��������Σ�����GM=GD���Ӷ��ó�
�ǵ��������Σ�����GM=GD���Ӷ��ó�![]() �ǵȱ������Σ���3�����ƣ�1����2���з������ȵõ�
�ǵȱ������Σ���3�����ƣ�1����2���з������ȵõ�![]() �ǵ��������Σ�������GDM=��GEC=900���Ӷ��ó�
�ǵ��������Σ�������GDM=��GEC=900���Ӷ��ó�![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
���������
��1��֤�������ı���CEGH��CFMN��ȫ�ȵľ��Σ�
��CE= CF��EG=FM����GEC =��MFC = 90�㣮
����DE��DF����ͼ��
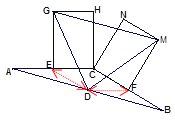
��D��E��F�ֱ���AB��AC��BC���е㣬
DE��BC����DE=CE =![]() BC��
BC��
DF��AC����DF = CE = ![]() AC��
AC��
���ı���DECF��ƽ���ı��Σ�
�� ��DEC=��DFC��
�֡ߡ�GEC=��MFC��
���DEG=��DFM��
��AC=BC��
��DE=DF.
���FBM�ա�MDH��SAS����
��DG=DM��
���DGM�ǵ��������Σ�
��2����DGM�ǵȱ������Σ�
֤������![]() ��
��![]() ��ȫ�ȵĵȱ������Σ�
��ȫ�ȵĵȱ������Σ�
��CE=EG=CG=CF=FM=CM����GEC=��MFC=60�㣮
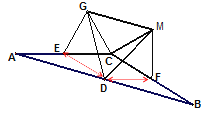
����DE��DF����ͼ��
��D��E��F�ֱ���AB��AC��BC���е㣬
��DE��BC����DE =CE =![]() BC��
BC��
DF��AC����DF=CE=![]() AC��
AC��
���ı���DECF��ƽ���ı��Σ�
�� ��DEC=��DFC��
�֡ߡ�GEC=��MFC��
���DEG=��DFM��
��AC=BC��
��DE=DF.
���FBM����MDH��SAS����
��DG=DM��
���DGM�ǵ��������Σ�
�֡ߡ�GCM+��ACB=3600-600-600=2400
��GED+��ACB=��GEC+��CED+��ACB=600+1800=2400
���GCM=��GED
��DE=CF=CM��EG=CG
���GED�ա�GCM��SAS����
��GM=GD
���DGM�ǵȱ������Σ�
��3����DGM�ǵ���ֱ�������Σ�
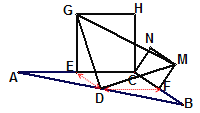
��Ȼ���ɣ�1����2������GED����DFM��SAS��
��DG=DM����DGE=��MDF
��DF��AC
���CED+��EDF=1800/p>
������CED+��EDG+��GDM+��MDF=1800
�����������ڽǺͿ�֪��CED+��EDG+��GEC+��DGE=1800
���GDM=��GEC=900
���DGM�ǵ���ֱ��������.


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ�ij������ͬѧ�ֱ������5�ζ���ѵ����Ҫ�ж���һ��ͬѧ�ijɼ��Ƚ��ȶ���ͨ����Ҫ�Ƚ�����ͬѧ�ɼ���( )
A. ƽ���� B. ���� C. Ƶ���ֲ� D. ��λ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD����һ��P���߳�Ϊ4���ҡ�PBC�ǵȱ������Σ����APD= �� S��APB= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ũҵũ�岿���Ų��칫��2018��10��15����Ϣ������ʡ�������Ʒ����������飬�˴��������鷢�����������ٶȿ죮����������ҵѸ�ٽ��������������Ŗ˺ʹ��ã��������Ŗ˹�����.ijũ����һ�췢��3ͷ��������.������ֹ���363ͷ������������ÿͷ��������ƽ��ÿ�촫Ⱦ����ͷ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ�ƽ�ơ�ABC��������ABC��һ������Aƽ�Ƶ���D����
��1����������ƽ�ƺ��ͼ�Ρ�DEF, 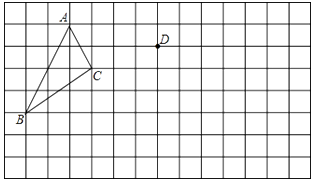
��2���������DEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P(x��3��2x��4)�ں����ϣ���x��ֵ��( )
A. ��3 B. ��2 C. 0 D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڦ�ABC�У���ABC�͡�ACB��ƽ���߽��ڵ�E������E��MN��BC��AB��M�� ��AC��N����BM+CN=9�����߶�MN�ij�Ϊ�� ��
A.6
B.7
C.8
D.9
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com