
【题目】如图,正方形ABCD中有一点P,边长为4,且△PBC是等边三角形,则∠APD= , S△APB= . 
【答案】150°;8﹣4 ![]()
【解析】解:作PM⊥AD,延长MP交BC于N. 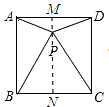
∵正方形ABCD中,∠ABC=90°,AD∥BC,AB=BC=CD
∴MN⊥BC,
∵△BCP为等边三角形,
∴∠PBC=60°,AB=BP=BC=CD,
∴∠ABP=30°∴∠BAP=75°,
∴∠DAP=15°,同理∠ADP=15°,
∴∠APD=150°.
∵PN= ![]() ×4=2
×4=2 ![]() ,
,
∴PM=4﹣2 ![]() ,
,
S△APD= ![]() ×4×(4﹣2
×4×(4﹣2 ![]() )=8﹣4
)=8﹣4 ![]() .
.
所以答案是 150°,8﹣4 ![]() .
.
【考点精析】关于本题考查的等边三角形的性质和正方形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).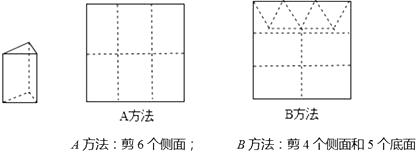
现有19张硬纸板,裁剪时 x 张用A方法,其余用B方法.
(1)分别求裁剪出的侧面和底面的个数(用含 x 的式子表示);
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
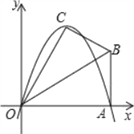
查看答案和解析>>
科目:初中数学 来源: 题型:
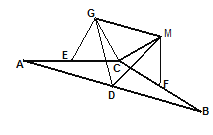
【题目】已知,如图,在![]() 中,AC=BC,点D是边AB的中点,E,F分别是AC和BC的中点,分别以CE,CF为一边向上作两个全等的矩形CEGH和矩形CFMN(其中EG=FM),依次连结DG、DM、GM。
中,AC=BC,点D是边AB的中点,E,F分别是AC和BC的中点,分别以CE,CF为一边向上作两个全等的矩形CEGH和矩形CFMN(其中EG=FM),依次连结DG、DM、GM。
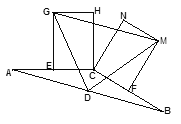
(1)求证:![]() 是等腰三角形。
是等腰三角形。
(2)如图,若将上图中的两个全等的矩形改为两个全等的正三角形(![]() 和
和![]() ),其他条件不变。请探究
),其他条件不变。请探究![]() 的形状,并说明理由。
的形状,并说明理由。
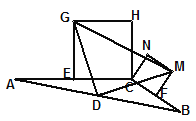
(3)若将上图中的两个全等的矩形改为两个正方形,并把![]() 中的边BC缩短到如图形状,请探究
中的边BC缩短到如图形状,请探究![]() 的形状,并说明理由。
的形状,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个长方体的长为2a , 宽也是2a , 高为h.
(1)用a 、h的代数式表示该长方体的体积与表面积. ![]()
(2)当a=3,h= ![]() 时,求相应长方体的体积与表面积.
时,求相应长方体的体积与表面积.
(3)在(2)的基础上,把长增加x , 宽减少x , 其中0<x<6,问长方体的体积是否发生变化,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com