
【题目】综合与探究
数学课上,老师让同学们利用三角形纸片进行操作活动,探究有关线段之间的关系.
问题情境:
如图1,三角形纸片ABC中,∠ACB=90°,AC=BC.将点C放在直线l上,点A,B位于直线l的同侧,过点A作AD⊥l于点D.
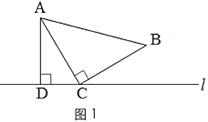
初步探究:
(1)在图1的直线l上取点E,使BE=BC,得到图2.猜想线段CE与AD的数量关系,并说明理由;
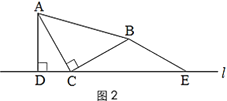
变式拓展:
(2)小颖又拿了一张三角形纸片MPN继续进行拼图操作,其中∠MPN=90°,MP=NP.小颖在图 1 的基础上,将三角形纸片MPN的顶点P放在直线l上,点M与点B重合,过点N作NH⊥l于点 H.
请从下面 A,B 两题中任选一题作答,我选择_____题.
A.如图3,当点N与点M在直线l的异侧时,探究此时线段CP,AD,NH之间的数量关系,并说明理由.
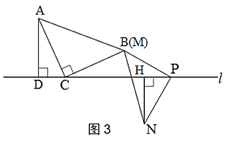
B.如图4,当点N与点M在直线l的同侧,且点P在线段CD的中点时,探究此时线段CD,AD,NH之间的数量关系,并说明理由.
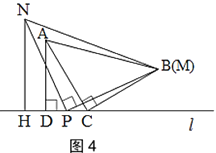
【答案】(1)CE=2AD;(2)A题:CP=AD+NH;B题:NH=![]() CD+AD.
CD+AD.
【解析】
(1) 过点B作BF⊥l于点F,通过已知条件证得△ACD≌△CBF,再通过等腰三角形性质即可求解.
(2) ①过点B作BF⊥l于点F,通过已知条件△ACD≌△CBF证得△BFP≌△PHN,即可得出边边之间关系.
②过点B作BF⊥l于点F,通过已知条件△ACD≌△CBF证得△BFP≌△PHN,再通过边边转化即可求解.
(1)CE=2AD,理由如下:
过点B作BF⊥l于点F,易得∠CFB=90°
∵AD⊥l
∴∠ADC=90°,∠CAD+∠DCA=90°
∴∠ADC=∠CFB
∵∠ACB=90°
∴∠DCA+∠BCF=90°
∴∠CAD=∠BCF
在△ACD和△CBF 中
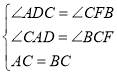
∴△ACD≌△CBF(AAS)
∴AD=CF
∵BE=BC,BF⊥l
∴CF=EF
∴CE=2CF=2AD
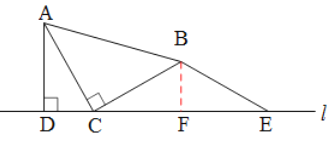
(2)A.CP=AD+NH,理由如下:
过点B作BF⊥l于点F,易得∠BFP=90°,
由(1)可得:△ACD≌△CBF
∴AD=CF
∵NH⊥l
∴∠PHN=90°,∠HNP+∠HPN=90°
∴∠BFP=∠PHN
∵∠MPN=90°
∴∠HPN+∠FPB=90°
∴∠HNP=∠FPB
在△BFP和△PHN 中

∴△BFP≌△PHN(AAS)
∴NH=PF
∵CP=CF+PF
∴CP=AD+NH
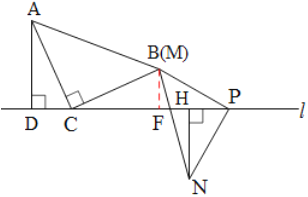
B.NH=![]() CD+AD,理由如下:
CD+AD,理由如下:
过点B作BF⊥l于点F,易得∠BFC=90°,
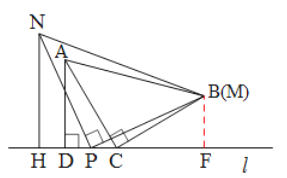
由(1)可得:△ACD≌△CBF
∴AD=CF
∵NH⊥l
∴∠PHN=90°,∠HNP+∠HPN=90°
∴∠BFP=∠PHN
∵∠MPN=90°
∴∠HPN+∠FPB=90°
∴∠HNP=∠FPB
在△BFP 和△PHN中

∴△BFP≌△PHN(AAS)
∴NH=PF
∵点P在线段CD的中点
∴CP=DP=![]() CD
CD
由图得:PF=PC+CF
∴NH=![]() CD+AD
CD+AD


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
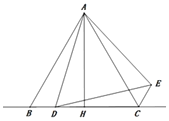
【题目】如图,在△ABC中,AB=AC,AH⊥BC,垂足为H,D为直线BC上一动点(不与点B、C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)求证:BD=CE;
(2)若点D在线段BC上,问点D运动到何处时,AC⊥DE?请说明理由;
(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数.(直接写出结果,无需写出求解过程)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某幼儿园计划购进一批甲、乙两种玩具,已知一件甲种玩具的价格与一件乙种玩具的价格的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的价格分别是多少元?
(2)该幼儿园计划用3500元购买甲、乙两种玩具,由于采购人员把甲、乙两种玩具的件数互换了,结果需4500元,求该幼儿园原计划购进甲、乙两种玩具各多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1,D三点的坐标分别是(0,4),(0,3),(0,2).
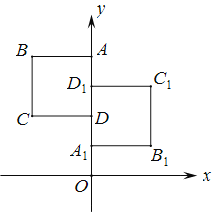
(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
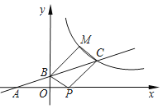
【题目】如图所示,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与反比例函
,与反比例函![]() 的图象交于点
的图象交于点![]() ,且
,且![]() .
.
(1)求点![]() 的坐标和反比例函数
的坐标和反比例函数![]() 的解析式;
的解析式;
(2)点![]() 在
在![]() 轴上,反比例函数
轴上,反比例函数![]() 图象上存在点
图象上存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形,求点M的坐标.
为平行四边形,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠A=∠B=70°.请按如下要求操作并解答:

(1)在图中,过点A画直线MP∥BC,过点C画直线NP⊥AB,直线MP与NP交于点P,求∠APC的度数;
(2)在(1)的前提下,直线PM上存在点D,且∠ABD=∠ADB,求直线BD与直线PN相交所形成的锐角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第100个图中正方形和等边三角形的个数之和是( )

A. 900 B. 903 C. 906 D. 807
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com