
 如图,一次函数y=x-2图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(3,m),与x轴交于点B.
如图,一次函数y=x-2图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(3,m),与x轴交于点B.分析 (1)由点A(3,m)在直线y=x-2上,求得m=3-2=1,得到A(3,1),把点A(3,1)代入y=$\frac{k}{x}$(x>0)中即可得到结论;
(2)求出直线y=x-2与x轴的交点B(2,0),即可得到结论.
解答 解:(1)∵点A(3,m)在直线y=x-2上,
∴m=3-2=1,
∴A(3,1),
∵点A(3,1)在y=$\frac{k}{x}$(x>0)的图象上,
∴1=$\frac{k}{3}$,∴k=3,
∴反比例函数的解析式为:y=$\frac{3}{x}$;
(2)∵直线y=x-2与x轴交于点B,
令y=0,得x=2,
∴B(2,0),∵A(3,1),
∴S△AOB=$\frac{1}{2}$×2×1=1.
点评 本题考查了一次函数与反比例函数的图象与性质,待定系数法求函数解析式,三角形面积的求法,注意数形结合思想在题目中的应用.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:解答题
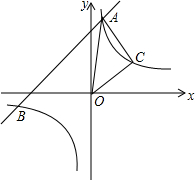 已知一次函数y1=x+5的图象与反比例函数${y_2}=\frac{m}{x}$的图象交于A、B两点,并且当x>1时,y1>y2;当0<x<1时,y1<y2.
已知一次函数y1=x+5的图象与反比例函数${y_2}=\frac{m}{x}$的图象交于A、B两点,并且当x>1时,y1>y2;当0<x<1时,y1<y2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小刚和小强相约晨练跑步,小刚比小强早1分钟离开家门,3分钟后迎面遇到从家跑来的小强.两人同路并行跑了2分钟后,决定进行长跑比赛,比赛时小刚的速度始终是180米/分,小强的速度始终是220米/分.下图是两人之间的距离y(米)与小刚离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题:
小刚和小强相约晨练跑步,小刚比小强早1分钟离开家门,3分钟后迎面遇到从家跑来的小强.两人同路并行跑了2分钟后,决定进行长跑比赛,比赛时小刚的速度始终是180米/分,小强的速度始终是220米/分.下图是两人之间的距离y(米)与小刚离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3).反比例函数y1=$\frac{k}{x}$图象经过点C,一次函数y2=ax+b的图象经过点A、C
如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3).反比例函数y1=$\frac{k}{x}$图象经过点C,一次函数y2=ax+b的图象经过点A、C查看答案和解析>>
科目:初中数学 来源: 题型:填空题
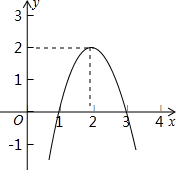 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象可知:方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为k<2.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象可知:方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为k<2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
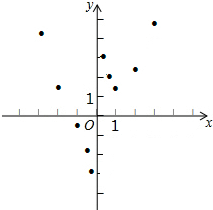 有这样一个问题:探究函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质.
有这样一个问题:探究函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质.| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | $\frac{25}{6}$ | $\frac{3}{2}$ | -$\frac{1}{2}$ | -$\frac{15}{8}$ | -$\frac{53}{18}$ | $\frac{55}{18}$ | $\frac{17}{8}$ | $\frac{3}{2}$ | $\frac{5}{2}$ | m | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m,AB和CD之间有一景观池,小南在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°(点B、E、D在同一直线上),求两幢建筑物之间的距离BD(结果精确到0.1m).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m,AB和CD之间有一景观池,小南在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°(点B、E、D在同一直线上),求两幢建筑物之间的距离BD(结果精确到0.1m).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com