
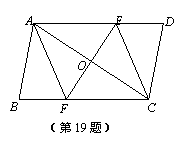
已知:如图,在□ABCD中,线段EF分别交AD、AC、BC于点E、O、F,
EF⊥AC,AO=CO.
(1)求证:△ABF≌△CDE;
(2)在本题的已知条件中,有一个条件如果去掉,并不影响(1)的证明,你认为这个多余的条件是 (直接写出这个条件).
 |
解:(1)∵四边形ABCD是平行四边形,
∴AB=CD,∠B=∠D,AD=BC,AD∥BC.
∵AD∥BC.
∴∠EAO=∠FCO,
又∵∠AOE=∠COF,
∴△AOE≌△COF.················································································· 3分
∴CF=AE,
∴AD-AE=BC-CF,
即DE=BF.
∵AB=CD,∠B=∠D,BF=DE,
∴△ABF≌△CDE.················································································· 5分
(2)EF⊥AC.······························································································ 7分


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
某商品的进价为每件40元,售价为每件50元,每个月可卖出210件.如果每件商品的售价每上涨1元,则每个月少卖10件.当每件商品的售价定为多少元时,每个月的利润恰为2200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
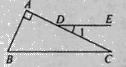
如右图,△ABC中,∠A=90°,点D在AC边上,DE∥BC,若
∠1=35°,则∠B的度数为 ( )
A.25° B.35° C.55° D.65°
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场新近一批A、B两种型号的节能防近视台灯,每台进价分别为200元、170元,近两周的销售情况如下:
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的台灯的销售单价;
(2)若该商场准备用不多于5400元的金额再购进这两种型号的台灯共30台,求A种型号的台灯最多能购进多少台?
(3)在(2)的条件下,该商场销售完这30台台灯能否实现利润为1400元的目标,若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com