
【题目】如图,正方形ABCD的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,点B在双曲线![]() (x<0)上,点D在双曲线
(x<0)上,点D在双曲线![]() (x>0)上,点D的坐标是 (3,3)
(x>0)上,点D的坐标是 (3,3)
(1)求k的值;
(2)求点A和点C的坐标.
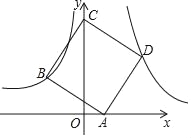
【答案】(1)k=9,(2)A(1,0), C(0,5).
【解析】
(1)根据反比例函数过点D,将坐标代入即可求值,(2)利用全等三角形的性质,计算AM,AN,CH的长即可解题.
解:将点D代入![]() 中,
中,
解得:k=9,
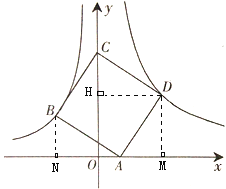
(2)过点B作BN⊥x轴于N, 过点D作DM⊥x轴于M,
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∵∠BAN+∠ABN=90°,
∴∠BAN=∠ADM,
∴△ABN≌△DAM(AAS),
∴DM=AN=3,
设A(a,0),
∴N(a-3,0),
∵B在![]() 上,
上,
∴BN=![]() =AM,
=AM,
∵OM=a![]() =3,整理得:a2-6a+5=0,
=3,整理得:a2-6a+5=0,
解得:a=1或a=5(舍去),
经检验,a=1是原方程的根,
∴A(1,0),
过点D作DH⊥Y轴于H,
同理可证明△DHC≌△DMA,
∴CH=AM=2,
∴C(0,5),
综上, A(1,0), C(0,5).


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
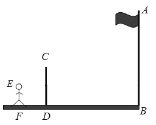
【题目】如图,九(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,人的眼睛E、标杆顶点C和旗杆顶点A在同一直线,求旗杆AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
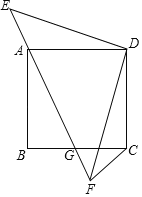
【题目】如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
①求证:△DAE≌△DCF;
②求证:△ABG∽△CFG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,过点C(1,2)分别作x轴、y轴的平行线,交直线y=﹣x+8于A、B两点,若反比例函数y=![]() (x>0)的图象与△ABC有公共点,则k的取值范围是( )
(x>0)的图象与△ABC有公共点,则k的取值范围是( )
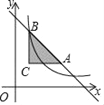
A. 2≤k≤12 B. 2≤k≤7 C. 7≤k≤12 D. 2≤k≤16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张正方形纸片ABCD对折,使CD与AB重合,得到折痕MN后展开,E为CN上一点,将△CDE沿DE所在的直线折叠,使得点C落在折痕MN上的点F处,连接AF,BF,BD.则下列结论中:①△ADF是等边三角形;②tan∠EBF=2-![]() ;③S△ADF=
;③S△ADF=![]() S正方形ABCD;④BF2=DF·EF.其中正确的是( )
S正方形ABCD;④BF2=DF·EF.其中正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直角梯形OABC中,CB∥OA,对角线OB和AC交于点D,OC=2,CB=2,OA=4,点P为对角线CA上的一点,过点P作QH⊥OA于H,交CB的延长线于点Q,连接BP,如果△BPQ和△PHA相似,则点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.
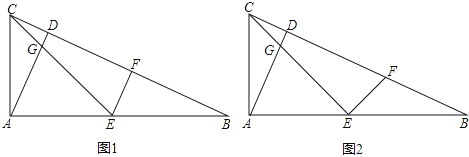
(1)如图1,AC:AB=1:2,EF⊥CB,求证:EF=CD.
(2)如图2,AC:AB=1:![]() ,EF⊥CE,求EF:EG的值.
,EF⊥CE,求EF:EG的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com