
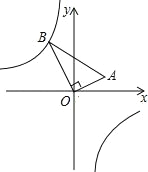
【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(4,2),BO=4![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点B,则k的值为_____.
的图象经过点B,则k的值为_____.
【答案】﹣32
【解析】
根据∠AOB=90°,过点A作AC⊥x轴,过点B作BD⊥x轴,证明△DBO∽△COA,再利用相似三角形的对应边成比例,列出比例式进行计算,求得点B的坐标,进而得出k的值.
过点A作AC⊥x轴,过点B作BD⊥x轴,垂足分别为C、D,则∠OCA=∠BDO=90°,
∴∠DBO+∠BOD=90°,
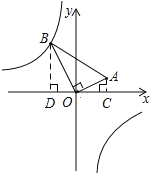
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠DBO=∠AOC,
∴△DBO∽△COA,
∴![]() ,
,
∵点A的坐标为(4,2),
∴AC=2,OC=4,
∴AO=![]() ,
,
∴![]() ,即BD=8,DO=4,
,即BD=8,DO=4,
∴B(-4,8),
∵反比例函数y=![]() 的图象经过点B,
的图象经过点B,
∴k的值为-4×8=-32.
故答案为:-32.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成长方形零件PQMN,使长方形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上,求这个长方形零件PQMN面积S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:
①∠ADE=∠DBF;②△DAE≌△BDG;③若AF=2DF,则BG=6GF;④CG与BD一定不垂直;⑤∠BGE=60°.其中正确的结论个数为( )
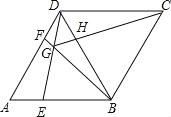
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”.比赛项目为:![]() .唐诗;
.唐诗;![]() .宋词;
.宋词;![]() .论语;
.论语;![]() .三字经.比赛形式分“单人组”和“双人组”.
.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则小红和小明都没有抽到“论语”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在函数y=![]() (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).
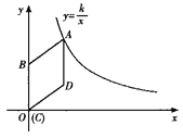
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=![]() (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形OBDC的对角线相交于点E,其中O(0,0),B(3,4),C(m,0),反比例函数y=![]() (k≠0)的图象经过点B.
(k≠0)的图象经过点B.
(1)求反比例函数的解析式;
(2)若点E恰好落在反比例函数y=![]() 上,求平行四边形OBDC的面积.
上,求平行四边形OBDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,E是正方形ABCD的边BC上任意一点,过点A作FA⊥AE于A,与CD的延长线交于点F,求证:AE=AF;
(2)如图②,当点E是正方形ABCD的边BC延长线上的任意一点时,过点A作FA⊥AE于A,交CD的延长线于点F.结论AE=AF是否仍成立?若成立,请给予证明;若不成立,请说明理由.
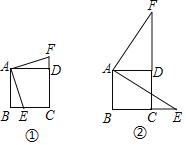
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若我们规定三角“![]() ”表示为:abc;方框“
”表示为:abc;方框“![]() ”表示为:(xm+yn).例如:
”表示为:(xm+yn).例如:![]() =1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
=1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
(1)计算:![]() = ______ ;
= ______ ;
(2)代数式 为完全平方式,则k= ______ ;
为完全平方式,则k= ______ ;
(3)解方程:![]() =6x2+7.
=6x2+7.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com