
【题目】如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成长方形零件PQMN,使长方形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上,求这个长方形零件PQMN面积S的最大值.

【答案】这个长方形零件PQMN面积S的最大值是2400mm2
【解析】试题分析:设长方形零件PQMN的边PN=a,PQ=x,则AE=80﹣x,利用△APN∽△ABC得相似比,用相似比可得出用含x的式子表示a,故S=xa,从而得出二次函数解析式,根据解析式及自变量取值范围求S的最大值.
试题解析:设长方形零件PQMN的边PN=a,PQ=x,则AE=80﹣x. ∵PN∥BC,
∴△APN∽△ABC.
∴ ![]() =
= ![]() .
.
因此, ![]() =
= ![]() .
.
解得a=120﹣ ![]() x.
x.
所以长方形PQMN的面积S=xa=x(120﹣ ![]() x)=﹣
x)=﹣ ![]() x2+120x.
x2+120x.
当x=﹣ 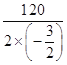 =40时,a=60.
=40时,a=60.
S最大值=40×60=2400(mm2).
所以这个长方形零件PQMN面积S的最大值是2400mm2.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB 所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2= 17, 且线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根.
(1)求C点的坐标;
(2)以斜边AB为直径作圆与y轴交于另一点E,求过A、B、E 三点的抛物线的关系式,并画出此抛物线的草图.
(3)在抛物线上是否存在点P,使△ABP与△ABC全等?若存在,求出符合条件的P点的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各题合并同类项,结果正确的是( )
A.13ab﹣4ab=9
B.﹣5a2b﹣2a2b=﹣7a2b
C.﹣12a2+5a2=7a2
D.2x3+3x3=5x6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用反证法证明命题“钝角三角形中必有一个内角小于45°”时,首先应该假设这个三角形中( )
A. 有一个内角小于45° B. 每一个内角都小于45°
C. 有一个内角大于等于45° D. 每一个内角都大于等于45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com