
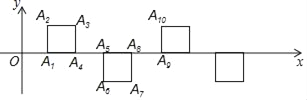
【题目】如图所示,在平面直角坐标系中,OA1=1,将边长为1的正方形一边与x轴重合按图中规律摆放,其中每两个正方形的间距都是1,则点A2017的坐标为 .
【答案】(1009,0)
【解析】试题解析:由图可得,第一个正方形中,A1(1,0),A2(1,1),A3(2,1),A4(2,0),各点的横坐标依次为1,1,2,2,纵坐标依次为0,1,1,0;
第二个正方形中,A5(3,0),A6(3,-1),A7(4,-1),A8(4,0),各点的横坐标依次为3,3,4,4,纵坐标依次为0,-1,-1,0;
根据纵坐标的变化规律可知,每8个点一次循环,
∵2016÷8=252,
∴点A2017在第253个循环中的第一个点的位置,故其纵坐标为0,
又∵A1的横坐标为1,A9的横坐标为5=1+4×1,A17的横坐标为9=1+4×2,…
∴A2017的横坐标为1+4×(253-1)=1009,
∴点A2017的坐标为(1009,0),
故答案为(1009,0)


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一点,联结
上一点,联结![]() ,以
,以![]() 为一边且在
为一边且在![]() 的右侧作正方形
的右侧作正方形![]() .
.
(1)如果![]() ,
,![]() ,
,
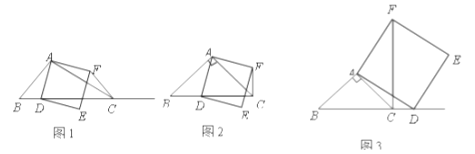
①当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),如图2,线段
不重合),如图2,线段![]() 所在直线的位置关系为 ,线段
所在直线的位置关系为 ,线段![]() 的数量关系为 ;
的数量关系为 ;
②当点![]() 在线段
在线段![]() 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果![]() ,
,![]() 是锐角,点
是锐角,点![]() 在线段
在线段![]() 上,当
上,当![]() 满足什么条件时,
满足什么条件时,![]() (点
(点![]() 不重合),并说明理由.
不重合),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为准备参加某市2019年度中小学生机器人竞赛,学校对甲、乙两支机器人制作小队所创作的机器人分别从创意、设计、编程与制作三方面进行量化,各项量化满分100分,根据量化结果择优推荐.它们三项量化得分如下表:
量化项目 | 量化得分 | |
甲队 | 乙队 | |
创意 | 85 | 72 |
设计 | 70 | 66 |
编程与制作 | 64 | 84 |
(1)如果根据三项量化的平均分择优推荐,哪队将被推荐参赛?
(2)根据本次中小学生机器人竞赛的主题要求,如果学校根据创意、设计、编程与制作三项量化得分按![]() 的比例确定每队最后得分的平均分择优推荐,哪队将被推荐参赛?并对另外一队提出合理化的建议.
的比例确定每队最后得分的平均分择优推荐,哪队将被推荐参赛?并对另外一队提出合理化的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
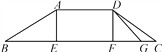
【题目】为了方便行人,市政府打算修建如图所示的过街天桥,桥面AD平行于地面BC,立柱AE⊥BC于点E,立柱DF⊥BC于点F,若AB=5![]() 米,tanB=
米,tanB=![]() ,∠C=30°.
,∠C=30°.
(1)求桥面AD与地面BC之间的距离.
(2)因受地形限制,决定对该天桥进行改建,使CD斜面的坡度变陡,将其30°坡角改为40°,改建后斜面为DG,试计算此次改建节省路面宽度CG大约应是多少?(结果精确到0.1米,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
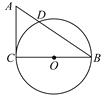
【题目】如图,在Rt△ACB中,∠C=90°,AC=3 cm,BC=4 cm,以BC为直径作⊙O交AB于点D.
(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问当点E在什么位置时,直线ED与⊙O相切?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为培养学生自主意识,拓宽学生视野,促进学习与生活的深度融合我市某中学决定组织部分学生去青少年综合实践基地进行综合实践活动在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生现有甲、乙两种大客车它们的载客量和租金如表所示
甲种客车 | 乙种客车 | |
载客量(人/辆) | 30 | 42 |
租金(元/辆) | 300 | 400 |
学校计划此实践活动的租车总费用不超过3100元,为了安全每辆客车上至少要有2名老师.
(1)参加此次综合实践活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,租用客车总数为多少辆?
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
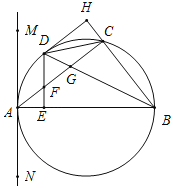
【题目】如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.
(1)求证:MN是半圆的切线;
(2)作DH⊥BC交BC的延长线于点H,连接CD,试判断线段AE与线段CH的数量关系,并说明理由.
(3)若BC=4,AB=6,试求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com