
����Ŀ����ͼ����֪AM��BN����A=60�㣮��P������AM��һ���㣨���A���غϣ���BC��BD�ֱ�ƽ�֡�ABP�͡�PBN���ֱ�����AM�ڵ�C��D�� 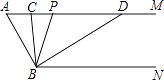
��1���١�ABN�Ķ������� �ڡ�AM��BN�����ACB=����
��2�����CBD�Ķ�����
��3������P�˶�ʱ����APB���ADB֮���������ϵ�Ƿ���֮�����仯�������仯����д������֮��Ĺ�ϵ����˵�����ɣ����仯����д���仯���ɣ�
��4������P�˶���ʹ��ACB=��ABDʱ����ABC�Ķ����� ��
���𰸡�
��1��120�㣻CBN
��2���⣺��AM��BN��
���ABN+��A=180�㣬
���ABN=180�㩁60��=120�㣬
���ABP+��PBN=120�㣬
��BCƽ�֡�ABP��BDƽ�֡�PBN��
���ABP=2��CBP����PBN=2��DBP��
��2��CBP+2��DBP=120�㣬
���CBD=��CBP+��DBP=60��
��3���⣺���䣬��APB����ADB=2��1��
��AM��BN��
���APB=��PBN����ADB=��DBN��
��BDƽ�֡�PBN��
���PBN=2��DBN��
���APB����ADB=2��1
��4��30��
���������⣺��1���١�AM��BN����A=60�㣬 ���A+��ABN=180�㣬
���ABN=120�㣻�ڡ�AM��BN��
���ACB=��CBN��
�ʴ�Ϊ��120�㣬��CBN����4����AM��BN��
���ACB=��CBN��
����ACB=��ABDʱ�����С�CBN=��ABD��
���ABC+��CBD=��CBD+��DBN��
���ABC=��DBN��
�ɣ�1����֪��ABN=120�㣬��CBD=60�㣬
���ABC+��DBN=60�㣬
���ABC=30�㣬
�ʴ�Ϊ��30�㣮
��1����ƽ���ߵ����ʣ���ֱ��ƽ��ͬ���ڽǻ������ڴ�����ȿɵã���2���ɣ�1��֪��ABP+��PBN=120�㣬�ٸ��ݽ�ƽ���ߵĶ���֪��ABP=2��CBP����PBN=2��DBP���ɵ�2��CBP+2��DBP=120�㣬����CBD=��CBP+��DBP=60�㣻��3����AM��BN�á�APB=��PBN����ADB=��DBN������BDƽ�֡�PBN֪��PBN=2��DBN���Ӷ��ɵá�APB����ADB=2��1����4����AM��BN�á�ACB=��CBN������ACB=��ABDʱ�С�CBN=��ABD���á�ABC+��CBD=��CBD+��DBN������ABC=��DBN�����ݡ�ABN=120�㣬��CBD=60��ɵô𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�� 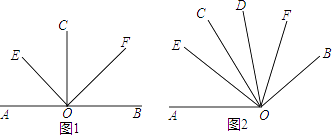
��1����ͼ1����CO��AB������ΪO��OE��OF�ֱ�ƽ�֡�AOC���BOC�����EOF�Ķ�����
��2����ͼ2������AOC=��BOD=80�㣬OE��OF�ֱ�ƽ�֡�AOD���BOC�����EOF�Ķ�����
��3������AOC=��BOD=��������BOD�Ƶ�O��ת��ʹ������OC������OD�ļн�Ϊ�£�OE��OF�ֱ�ƽ�֡�AOD���BOC������+�¡�180�㣬�����£����EOC= �� ���ú�����µĴ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(12��)��ͼ���ڡ�ABC������A��60�㣬��D��BC�ߵ��е���DE��BC����ABC��ƽ����BF��DE�ڡ�ABC��һ��P������PC.
(1)����ACP��24�㣬���ABP�Ķ�����
(2)����ACP��m�㣬��ABP��n�㣬��ֱ��д��m��n����Ĺ�ϵʽ��_________________��
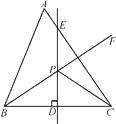
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������������a��b��c����(a+b)2=c2+2ab���������������( )
A. �ȱ������� B. �۽������� C. ����ֱ�������� D. ֱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������������ǣ�������
A.����ε��ڽǺ�Ϊ360��
B.��2a��b��1�������ʽ6a��3b��3��0
C.���κ���y����x��1��2+2��ͼ����y��Ľ��������Ϊ��0��2��
D.���εĶԽ����ഹֱƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB=AC����BAC=120����AD��AB��AE��AC��
��1����֤����ABE�ա�ACD��
��2����֤����ADE�ǵȱ������Σ�
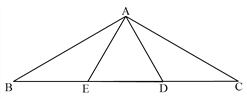
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A. һ����ǵ���DZ�����ǵIJ���С90����
B. ���һ�����в��ǣ���ô����DZ��Ƕ۽ǣ�
C. ����1+��2+��3=180�㣬���1����2����3��Ϊ���ǣ�
D. ����Ϧ��͡Ϧ»�Ϊ��ǣ��Ϧ���ϦȻ�Ϊ��ǣ���ô�Ϧ���ϦȻ�Ϊ��ǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=90�㣬��AOCΪ��AOB���һ����ǣ��ҡ�AOC=30�㣬����OMƽ�֡�BOC��ONƽ�֡�AOC�� 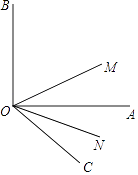
��1�����MON�Ķ�����
��2�������1���С�AOB=���������������䣬���MON�Ķ�����
��3�������1���С�AOC=�£���Ϊ��ǣ��������������䣬���MON�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ι��ţ�����������ˮ��2mʱ��ˮ���4m����ˮ���½���2.5m��ˮ��Ŀ������Ӷ��٣�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com