
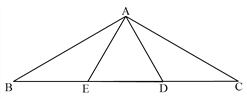
【题目】如图,AB=AC,∠BAC=120°,AD⊥AB,AE⊥AC.
(1)求证:△ABE≌△ACD;
(2)求证:△ADE是等边三角形.
【答案】见解析
【解析】试题分析:(1)利用两角及其夹边对应相等的两个三角形全(ASA)不难证明△ABE≌△ACD;由已知条件求出∠ADB =60°,∠AEC=60°,即可证明.
试题解析:
(1)证明∵AB=AC,
∴∠B=∠C,
∵AD⊥AB,AE⊥AC,
∴∠BAD=∠CAE =90°,
∴∠BAE=∠CAD,
∵在△ABE和△ACD中
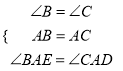 ,
,
∴△ABE≌△ACD (ASA);
(2)∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
在△ABD中,∠B=30°,∠BAD =90°,
∴∠ADB =60°,
同理∠AEC=60°,
∴∠ADB=∠AEC=∠EAD=60°,
∴△ADE是等边三角形.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】对于下列各组条件,不能判定△![]() ≌△
≌△![]() 的一组是 ( )
的一组是 ( )
A. ∠A=∠A′,∠B=∠B′,AB=A′B′
B. ∠A=∠A′,AB=A′B′,AC=A′C′
C. ∠A=∠A′,AB=A′B′,BC=B′C′
D. AB=A′B′,AC=A′C′,BC=B′C′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D. 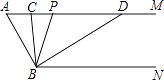
(1)①∠ABN的度数是; ②∵AM∥BN,∴∠ACB=∠;
(2)求∠CBD的度数;
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题.
(1)已知一个多边形的内角和是1260°,求这个多边形的边数.
(2)用一条长为18cm的细绳围成一个等腰三角形,若有一边长等于4cm,求另外两边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解不等式![]() 的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
解:去分母,得3(1+x)-2(2x+1)≤1.①
去括号,得3+3x-4x+1≤1.②
移项,得3x-4x≤1-3-1.③
合并同类项,得-x≤-3.④
两边都除以-1,得x≤3.⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.
(1)数轴上点A表示的数为
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S. ①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数为 .
②设点A的移动距离AA′=x.
ⅰ.当S=4时,x=;
ⅱ.D为线段AA′的中点,点E在线段OO′上,且OE= ![]() OO′,当点D,E所表示的数互为相反数时, x=
OO′,当点D,E所表示的数互为相反数时, x=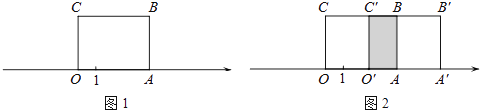
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于n的函数s=an2+bn(n为自然数),当n=9时,s<0;当n=10时,s>0.则n取( )时,s的值最小.
A.3B.4C.5D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com