
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.
(1)数轴上点A表示的数为
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S. ①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数为 .
②设点A的移动距离AA′=x.
ⅰ.当S=4时,x=;
ⅱ.D为线段AA′的中点,点E在线段OO′上,且OE= ![]() OO′,当点D,E所表示的数互为相反数时, x=
OO′,当点D,E所表示的数互为相反数时, x=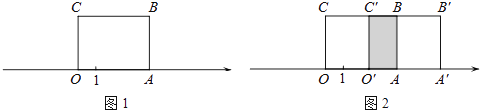
【答案】
(1)4
(2)6或2;![]() ;
;![]()
【解析】解:(1)∵长方形OABC的面积为12,OC边长为3, ∴OA=12÷3=4,
∴数轴上点A表示的数为4,
所以答案是:4. (2)①∵S恰好等于原长方形OABC面积的一半,
∴S=6,
∴O′A=6÷3=2,
当向左运动时,如图1,A′表示的数为2
当向右运动时,如图2,
∵O′A′=AO=4,
∴OA′=4+4﹣2=6,
∴A′表示的数为6,
所以答案是:6或2.②ⅰ.如图1,由题意得:COOA′=4,
∵CO=3,
∴OA′= ![]() ,
,
∴x=4﹣ ![]() =
= ![]() ,
,
所以答案是: ![]() ;
;
ⅱ.如图1,当原长方形OABC向左移动时,点D表示的数为 ![]() ,点E表示的数为
,点E表示的数为 ![]() ,
,
由题意可得方程:4﹣ ![]() x﹣
x﹣ ![]() x=0,
x=0,
解得:x= ![]() ,
,
如图2,当原长方形OABC向右移动时,点D,E表示的数都是正数,不符合题意.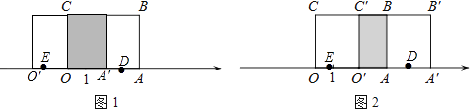
【考点精析】通过灵活运用数轴和平移的性质,掌握数轴是规定了原点、正方向、单位长度的一条直线;①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等即可以解答此题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,∠AOC为∠AOB外的一个锐角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC. 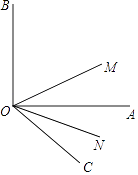
(1)求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠AOC=β(β为锐角),其他条件不变,求∠MON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知0<a<1,-1<b<0,那么在代数式a-b,a+b,a+b2,a2+b中,对任意的a、b,对应的代数式的值最大的是( )
A. a+b B. a-b C. a+b2 D. a2+b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,墙面OC与地面OD垂直,一架梯子AB长5米,开始时梯子紧贴墙面,梯子顶端A沿墙面匀速每分钟向下滑动1米,x分钟后点A滑动到点A′,梯子底端B沿地面向左滑动到点B′,OB′=y米,滑动时梯子长度保持不变.
(1)当x=1时,y= 米;
(2)求y关于x的函数关系式,并写出自变量x的取值范围;
(3)研究(2)中函数图象及其性质.
①填写下表,并在所给的坐标系中画出函数图象;
②如果点P(x,y)在(2)中的函数图象上,求证:点P到点Q(5,0)的距离是定值;
(4)梯子底端B沿地面向左滑动的速度是
A.匀速 B.加速 C.减速 D.先减速后加速.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】延庆区某中学七年级(1)(2)两个班共104人,要去延庆地质博物馆进行社会大课堂活动,老师指派小明到网上查阅票价信息,小明查得票价如图: 
其中(1)班不足50人,经估算,如果两个班都以班为单位购票,一共应付1240元.
(1)两个班各有多少学生?
(2)如果两个班联合起来,作为一个团体购票,可以省多少钱?
(3)如果七年级(1)班单独组织去博物馆参观,你认为如何购票最省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com