
【题目】如图,墙面OC与地面OD垂直,一架梯子AB长5米,开始时梯子紧贴墙面,梯子顶端A沿墙面匀速每分钟向下滑动1米,x分钟后点A滑动到点A′,梯子底端B沿地面向左滑动到点B′,OB′=y米,滑动时梯子长度保持不变.
(1)当x=1时,y= 米;
(2)求y关于x的函数关系式,并写出自变量x的取值范围;
(3)研究(2)中函数图象及其性质.
①填写下表,并在所给的坐标系中画出函数图象;
②如果点P(x,y)在(2)中的函数图象上,求证:点P到点Q(5,0)的距离是定值;
(4)梯子底端B沿地面向左滑动的速度是
A.匀速 B.加速 C.减速 D.先减速后加速.

【答案】(1)3(2)![]() (3)①表格见解析②P到点Q(5,0)的距离是定值(4)C
(3)①表格见解析②P到点Q(5,0)的距离是定值(4)C
【解析】
试题分析:(1)在Rt△A′OB′中,根据勾股定理求出OB′即可.
(2)在Rt△A′OB′中,根据勾股定理即可解决问题,再根据题意写出自变量的取值范围.
(3)①先列表,再画出图象即可.②利用两点间距离公式即可解决问题.
(4)如图2中,在半径OQ上取AB=BC,过A、B、C作x轴的垂线交圆弧于D、E、F,作DM⊥BE,EN⊥CF,延长DE交CF于G,只要证明EM>FN即可解决问题.
试题解析:(1)x=1时,A′B=5﹣1=4,A′B′=5,
∵∠O=90°,
∴y=OB′=![]() =3.
=3.
故答案为3.
(2)![]() ,(0≤x≤5).
,(0≤x≤5).
(3)①填表:
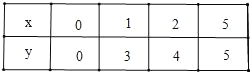
②图象如图所示:
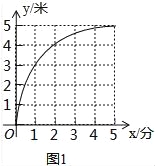
∵![]() ,
,
∴y2+(5﹣x)2=52,
即PQ2=PR2+RQ2=25,
∴PQ=5,
∴P到点Q(5,0)的距离是定值
(4)与(3)可知,函数图象是以Q为圆心的圆弧,
如图2中,在半径OQ上取AB=BC,过A、B、C作x轴的垂线交圆弧于D、E、F,作DM⊥BE,EN⊥CF,延长DE交CF于G.那么GN=EM,
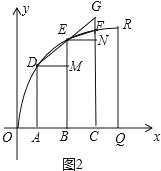
∵GN>FN,
∴EM>FN,
即点A移动的距离大于点B移动的距离,
∴是减速,
故选C.


科目:初中数学 来源: 题型:
【题目】小明解不等式![]() 的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
解:去分母,得3(1+x)-2(2x+1)≤1.①
去括号,得3+3x-4x+1≤1.②
移项,得3x-4x≤1-3-1.③
合并同类项,得-x≤-3.④
两边都除以-1,得x≤3.⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.
(1)数轴上点A表示的数为
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S. ①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数为 .
②设点A的移动距离AA′=x.
ⅰ.当S=4时,x=;
ⅱ.D为线段AA′的中点,点E在线段OO′上,且OE= ![]() OO′,当点D,E所表示的数互为相反数时, x=
OO′,当点D,E所表示的数互为相反数时, x=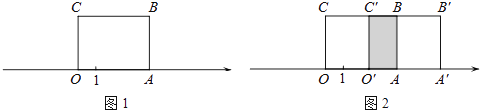
查看答案和解析>>
科目:初中数学 来源: 题型:
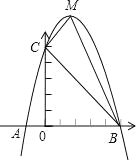
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积![]() .
.
(3)在坐标轴上,是否存在点N,满足△BCN为直角三角形?如存在,请直接写出所有满足条件的点N.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于n的函数s=an2+bn(n为自然数),当n=9时,s<0;当n=10时,s>0.则n取( )时,s的值最小.
A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b在数轴上的表示如图所示,则下列结论中:①ab<0,② ![]() ,③a+b<0, ④a﹣b<0,⑤a<|b|,⑥﹣a>﹣b,正确的有( )
,③a+b<0, ④a﹣b<0,⑤a<|b|,⑥﹣a>﹣b,正确的有( )![]()
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com