
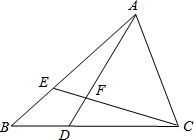
如图,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于点F,试判断△AFC的形状,并说明理由.
【考点】等腰三角形的判定;全等三角形的判定与性质.
【专题】探究型.
 【分析】要判断△AFC的形状,可通过判断角的关系来得出结论,那么就要看∠FAC和∠FCA的关系.因为∠BAD=∠BCE,因此我们只比较∠BAC和∠BCA的关系即可.根据题中的条件:BD=BE,∠BAD=∠BCE,△BDA和△BEC又有一个公共角,因此两三角形全等,那么AB=AC,于是∠BAC=∠BCA,由此便可推导出∠FA
【分析】要判断△AFC的形状,可通过判断角的关系来得出结论,那么就要看∠FAC和∠FCA的关系.因为∠BAD=∠BCE,因此我们只比较∠BAC和∠BCA的关系即可.根据题中的条件:BD=BE,∠BAD=∠BCE,△BDA和△BEC又有一个公共角,因此两三角形全等,那么AB=AC,于是∠BAC=∠BCA,由此便可推导出∠FA C=∠FCA,那么三
C=∠FCA,那么三 角形AFC应该是个等腰三角形.
角形AFC应该是个等腰三角形.
【解答】解:△AFC是等腰三角形.理由如下:
在△BAD与△BCE中,
∵∠B=∠B(公共角),∠BAD=∠BCE,BD=BE,
∴△BAD≌△BCE(AAS),
∴BA=BC,∠BAD=∠BCE,
∴∠BAC=∠BCA,
∴∠BAC﹣∠BAD=∠BCA﹣∠BCE,即∠FAC=∠FCA.
∴AF=CF,
∴△AFC是等腰三角形.
【点评】本题考查了全等三角形的判定与性质及等腰三角形的判定等知识点,利用全等三角形来得出角相等是本题解题的关键.


科目:初中数学 来源: 题型:
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形.所以,当n=3时,m=1
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形,所以,当n=4时,m=0
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形,所以,当n=5时,m=1
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形,所以,当n=6时,m=1
综上所述,可得表①
| n | 3 | 4 | 5 | 6 |
| m | 1 | 0 | 1 | 1 |
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2)分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三
角形?(只需把结果填在表②中)
| n | 7 | 8 | 9 | 10 |
| m |
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,…
解决问题:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设n分别等于4k﹣1、4k、4k+1、4k+2,其中k是整数,把结果填在表 ③中)
| n | 4k﹣1 | 4k | 4k+1 | 4k+2 |
| m |
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)
其中面积最大的等腰三角形每个腰用了__________根木棒.(只填结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com